Organized by: Sino-Russian Mathematics Center Chengdu Base
Supported by: Sino-Russian Mathematics Center
Coordinators: Weinian Zhang (Sichuan University)
Baofu Wang (Sichuan University)
Secretaries : Rui Jiang (Sichuan University)
Haichao Xiong (Sichuan University)
Date: August 16, 2022 (Tuesday)
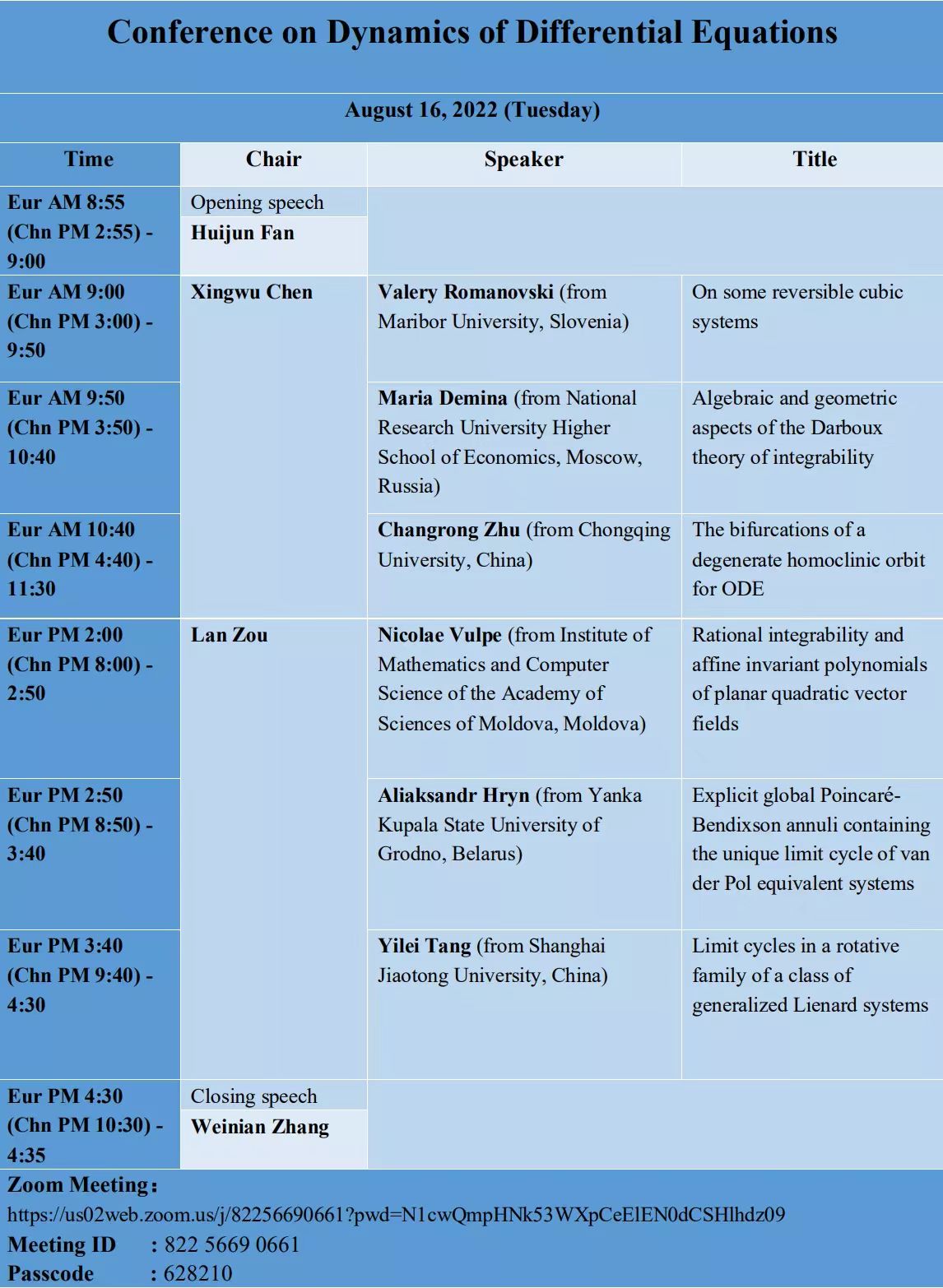
To Join Zoom Meeting:
https://us02web.zoom.us/j/82256690661?pwd=N1cwQmpHNk53WXpCeElEN0dCSHlhdz09
Meeting ID: 822 5669 0661
Passcode: 628210
Abstract and Introduction
Speaker: Valery Romanovski (Maribor University, Slovenia)
Valery Romanovski is a Professor at the University of Maribor and a Senior Researcher at the Center for Applied Mathematics and Theoretical Physics, University of Maribor, in Slovenia. He is a member of the European Academy of Sciences and Arts. His main research interests are in the fields of ordinary differential equations, dynamical systems, computational algebra, mathematical modeling, chemical and biological systems. He was awarded the State Prize of the Republic of Slovenia of the second degree for outstanding achievements in scientific research (Zoisovo priznanje).
Title: On some reversible cubic systems
Abstract: We study three systems from the classification of cubic reversible systems given by Żoła̧dek in 1994. Using affine transformations and elimination algorithms from these three families the six components of the center variety are derived and limit-cycle bifurcations in neighborhoods of the components are investigated. The invariance of the systems with respect to the generalized involutions introduced by Bastos, Buzzi and Torregrosa in 2021 is discussed. Computations are performed using the computer algebra systems Mathematica and Singular.
Speaker: Maria Demina (National Research University Higher School of Economics, Moscow, Russia)
Maria Demina is an Associate Professor at HSE University in Russia. Her Research interests include:
Ordinary differential equations (integrability, asymptotic analysis, meromorphic solutions, symmetries, Painlevé equations, equivalence problems), Nonlinear dynamical systems (integrability, numerical methods, regular and chaotic dynamics, stability, bifurcations), and Nonlinear mathematical models (solitary waves, point vortices, multi-particle dynamical systems).
Title: Algebraic and geometric aspects of the Darboux theory of integrability
Abstract: In 1878 Darboux connected the integrability of two-dimensional polynomial differential systems with the number and properties of their particular algebraic solutions. In recent years, the ideas of Darboux have been developed and extended to give rise to a theory now known as the Darboux theory of integrability. The aim of the talk is to present some modern aspects of this theory. The main difficulty in finding algebraic solutions lies in the fact that the degrees of their generating polynomials are not known in advance. I shall describe a method that can find all algebraic solutions for a great number of systems. This method makes finding algebraic solutions purely algebraic and is based on the properties of the asymptotic Puiseux series. In addition, I plan to present some applications and generalizations of the method.
Speaker: Changrong Zhu (Chongqing University, China)
Changrong Zhu is a professor at the College of Mathematics and Statistics, Chongqing University. He received a Master's degree from Chongqing University and PhD from Sichuan University. He works on ordinary differential equations. He was awarded Excellent Teacher of New Century by the Ministry of Education of the People's Republic of China.
Title: The bifurcations of a degenerate homoclinic orbit for ODE
Abstract: Consider an autonomous ordinary differential equation in R that has a homoclinic solution asymptotic to a hyperbolic equilibrium. The homoclinic solution is degenerate in the sense that the linear variational equation has d bounded, linearly independent solutions. We study bifurcation of the homoclinic solution under periodic perturbations. Using exponential dichotomies and Lyapunov-Schmidt reduction, we obtain general conditions under which the perturbed system can have transverse homoclinic solutions and nearby periodic or chaotic solutions.
Speaker: Nicolae Vulpe (Institute of Mathematics and Computer Science of the Academy of Sciences of Moldova, Moldova)
Nicolae Vulpe is a Principal Researcher at Vladimir Andrunachievici Institute of Mathematics and Computer Science, Academy of Science of Moldova. His main interests are the development of methods and algorithms for constructing polynomial bases of invariants for two-dimensional polynomial systems and their applications to the qualitative study of differential systems, essentially using computing algebra systems. In collaboration with specialists in the field from international centers of research such as UMontreal (Canada), UAB (Barcelona) and ICMC of the University of São Paulo (Brazil), various classifications of families of quadratic and cubic systems are performed.
Title: Rational integrability and affine invariant polynomials of planar quadratic vector fields
Abstract: In the first part of this talk we discuss the application of algebraic invariant theory to the classification of all quadratic differential systems having a rational first integral of degree 2. The constructed affine invariant criteria for characterization of this class of systems are given directly in the 12-dimensional space of the coefficients of quadratic systems and hence can be applied for any quadratic system in any canonical form. Moreover, the corresponding rational first integral of a system in this class is also given in invariant form and it can be determined for this system via a simple computation of the corresponding invariant polynomials.
In the second part of the talk, we are going to apply the invariant theory to give invariant conditions on the coefficients of any non-degenerate quadratic system in order to determine if it has or not a polynomial first integral without using any normal form. We show that the existence of polynomial first integral is directly related to the fact that all the roots of a convenient cubic polynomial with invariant coefficients are rational and negative.
Speaker: Aliaksandr Hryn (from Yanka Kupala State University of Grodno, Belarus)
Aliaksandr Hryn is the Head of the Department of Mathematical Analysis, Differential Equations and Algebra. His Interests and experiences are:
Qualitative theory and bifurcations theory of planar autonomous systems of differential equations including its applications. Analytic methods and numerical approaches to estimate the number and localization of limit cycles as well as to control some bifurcations of limit cycles in autonomous systems and their software realization.
Title: Explicit global Poincaré-Bendixson annuli containing the unique limit cycle of van der Pol equivalent systems
Abstract:
Speaker: Yilei Tang (from Shanghai Jiaotong University, China)
Yilei Tang, Professor of Shanghai Jiao Tong University, is mainly engaged in the research of qualitative theory and bifurcation theory of ordinary differential equations and dynamic systems. She’s supported by the National Natural Science Foundation of China (NSFC) for the General Program and Sub Project of Key Program; supported by European Union‘s Horizon 2020 programme under the Marie-Curie grant, and supported by the Ministry of Science and Technology of China(China-Slovenia). More than 40 papers are published in academic journals such as J. Differential Equations, Physica D, Nonlinearity, SIAM J. Appl. Math. and J. Nonlinear Sci.
Title: Limit cycles in a rotative family of a class of generalized Lienard systems
Abstract: In this talk, we study the problem of limit cycles in a rotative family of generalized Lienard systems allowing for finitely many switching lines. We can prove that some significant properties of analytic rotative vector fields remain true for the rotative family of generalized Lienard systems. Furthermore, we give the relation between variational exponent and multiplicity of limit cycles, which was not obtained for analytic rotative vector fields. Applying our results, we obtain the exact number of limit cycles and answer a question on the maximum number of limit cycles in a SD oscillator and a continuous piecewise linear system with three zones.