关于某些拟线性椭圆方程解的分类与刘维尔性质的新进展
Speaker: 王友德 (广州大学)
Time: 2026年1月8日, 10:00-11:00
Venue: 腾讯会议:290-429-573
Abstract:
我们将介绍定义在具非负里奇曲率的非紧完备流形上的拟线性退化Lane-Emden方程
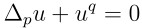
的最佳Liouville定理及如何使用Nash-Moser迭代获得一类拟线性退化椭圆方程正解的最佳形式的统一的郑-丘(Cheng-Yau)型梯度估计。我们也将介绍定义在里奇曲率非负的非紧黎曼流形上的临界p-Laplace方程正解的分类及刚性等。
Bio: 王友德,教授,博士生导师,国家杰出青年基金获得者,“百千万人才工程”国家级人选。在调和映射、几何流及其相关问题上进行了长期的研究,取得了一系列具有学术价值的成果。曾提出在国际上引发一系列后续研究的薛定谔几何流的概念及率先获得其局部适定性;解决了阿尔法调和映射序列收敛产生泡泡时能量恒等式是否成立等公开问题。
Previous lectures and talks:
Deformation quantization of the Loday-Quillen-Tsygan isomorphism
Speaker: Farkhod Eshmatov (New Uzbekistan University)
Time: December 24, 2025, 16:00-18:00
Venue: 吉林大学数学楼第五研讨室
Abstract:

Bio: Professor Farkhod Eshmatov is the Associate Dean of School of Natural Sciences and Humanity in New Uzbekistan University (Tashkent, Uzbekistan). He obtained his Ph.D in Mathematics at Cornell University in 2007. He mainly works on algebra, noncommutative algebraic geometry, integrable systems, infinite dimensional Lie algebras and mathematical physics. He has made many important works on noncommutative Poisson structure and symplectic structure, invariants of matrices, Calabi-Yau algebras, derived schemes, and so on. Recently, he and his coauthors introduced a novel approach that employs techniques from noncommutative Poisson geometry to comprehend the algebra of invariants of two matrices, and further entirely solved the open problem of computing the algebra of invariants of two matrices of order 4.
数学物理中的孤子模型介绍
Speaker: 乔志军 (德克萨斯大学)
Time: December 15, 2025, 16:00-18:00
Venue: 吉林大学数学楼第五研讨室
Abstract: 孤立子是自然界中十分奇特的现象,它们展现了由数学与物理基本原理所支配的复杂相互作用。通过本科普报告,可以以通俗易懂的方式初步了解孤立水波的基本模型及其重要意义。报告首先介绍孤立波的基本特征,强调它们即使在与其他波相互作用之后,仍能保持稳定的波形和恒定的传播速度。正是这些独特性质,使孤立波在理论研究和应用研究中都成为极具吸引力的课题。
我们回顾孤立波模型的发展历程,从 Korteweg-de Vries(KdV)方程出发,说明它如何为浅水中一维孤子行为提供基础性理解。KdV方程优美地刻画了非线性与色散之间的平衡,而这种平衡正是保持波动孤立结构的关键因素。此外,我们还将介绍更为复杂的模型,例如 Burgers 方程和 Camassa-Holm 方程,它们将对孤立波的理解拓展到更加复杂的浅水波环境之中。这些模型有助于揭示在不同物理背景下波的传播与相互作用所呈现的丰富动力学行为。报告最后还将简要介绍我们当前的数学与统计学跨学科应用博士项目,以及面向国际学生的助教(GTA)和助研(GRA)资助情况。
Bio: 乔志军博士,美国德克萨斯大学UTRGV讲席教授。1986-1989年获得郑州大学硕士学位,师从曹策问教授。1997年获得复旦大学博士学位,师从谷超豪院士和胡和生院士。主要从事非线性偏微分方程,可积系统与非线性尖孤波,KdV方程和孤立子理论,可积辛映射,R-矩阵理论,图像处理和数学物理的反问题等领域的研究。1999年获全国首届百篇优秀博士论文, 1999-2001年在德国Kassel大学任Humboldt学者。2013年获德克萨斯大学杰出研究奖,2016年被授予德克萨斯大学讲席教授, 2023年被授予Fulbright项目国际专家。主持完成国家级和国际级项目20余项。在国际一流期刊Communications in Mathematical Physics、IEEE Transaction on Geoscience and Remote Sensing (TGRS)等发表学术论文150多篇,出版著作2部。现任国际权威刊物Studies in Applied Mathematics编委和Journal of Nonlinear Mathematical Physics主编之一。
Hopf Algebroids from Dynamical Yang-Baxter Maps
Speaker: Youichi Shibukawa (Hokkaido University)
Time: December 11, 2025, 14:00-16:00
Venue: Zoom ID:904 645 6677, Password:2025
Link: https://zoom.us/j/9046456677?pwd=LJpBPzAw2Sn0MKhb0Qc6QdJ1jEeh7B.1&omn=88293207047
Abstract: Faddeev, Reshetikhin, and Takhtajan famously constructed q-analogs of function spaces, which are Hopf algebras (or, more precisely, bialgebras), by utilizing the R-matrices, solutions to the (quantum) Yang-Baxter equation. This talk introduces a generalization of their approach. We demonstrate that dynamical Yang-Baxter maps - solutions to a version of the dynamical Yang-Baxter equation - yield Hopf algebroids. These Hopf algebroids can also be regarded as a generalization of Hayashi's face algebras.
Bio: Professor Youichi Shibukawa is based at Hokkaido University. His initial research focused on the quantum group and its representation theory. He is currently studying Garside theoretic aspects of the quiver-theoretic Yang-Baxter equation.
Topological Recursion and Enumerative Geometry
Speaker: Bohan Fang (Peking University)
Time: November 27, 2025, 15:00-16:00
Venue: Zoom ID:904 645 6677, Password:2025
Link: https://zoom.us/j/9046456677?pwd=LJpBPzAw2Sn0MKhb0Qc6QdJ1jEeh7B.1&omn=88293207047
Abstract: Topological Recursion is an algorithm proposed by Chekhov-Eynard-Orantin, which associates a sequence of differential forms to a spectral curve. Originally motivated by matrix models, it has deep connection to various areas of mathematics, like enumerative geometry and integrable systems. I will give an introduction to Topological Recursion and explain some of its application in enumerative geometry. This talk is based on the joint work with Chiu-Chu Melissa Liu, Song Yu, and Zhengyu Zong.
Bio: 方博汉,北京大学博雅特聘教授。2005年本科毕业于北京大学,2010年博士毕业于美国西北大学,2014年开始在北京大学北京国际数学研究中心任职。研究方向为现代数学物理中的镜像对称和相关的几何学,其研究获得国家杰出青年科学基金资助,并且获17届中国青年科技奖。其研究论文发表在Invent. Math., JAMS.等杂志上。
Representations of nonnegative functions and global optimality conditions
Speaker: Tien-Son Pham (越南Dalat University)
Time: November 13, 15:00-16:00
Venue: 吉林大学正新楼306
Abstract:

Bio: Tien-Son Pham,越南Dalat University教授,博士生导师,长期从事奇异理论、半代数优化、变分分析等研究工作,在Mathematical Programming, SIAM Journal on Optimization, Mathematics of Operations Research等优化顶级期刊发表学术论文70余篇,出版学术专著1部。2020年获越南科技部颁发的Ta Quang Buu奖,并入选2021年度“亚洲百位杰出科学家”榜单(该榜单由亚洲科学家杂志自2016年起每年评选,表彰在科研领域取得重大突破或获得国家级/国际奖项的科学家)。现任越南高等数学研究所科学理事会(Scientific Council)成员。
Hurwitz problem on quadratic forms and composition algebras
Speaker: Maxim Goncharov (Sobolev Institute of Mathematics)
Time: November 12, 10:30-11:30
Venue: 吉林大学数学楼第五研讨室
Abstract: The original Hurwitz problem may be formulated as: given a natural number n and two sets of numbers x_1,...,x_n and y_1,...,y_n from a field F, is it possible to find elements z_1,...z_n from F such that
(x_1^2+x_2^2+...+x_n^2)(y_1^2+y_2^2+...y_n^2)=z_1^2+z_2^2+...+z_n^2?
For n=2, the positive solution of this question follows from the property of the module of complex numbers. In this talk, we will consider this problem in detail. Also, we will consider additional structures that appeared naturally while solving this problem (such as alternative and composition algebras, quaternions, and octonions).
Bio: Maxim Goncharov, Ph.D., Senior research fellow in Sobolev Institute of Mathematics, Associate Professor at Novosibirsk State University.
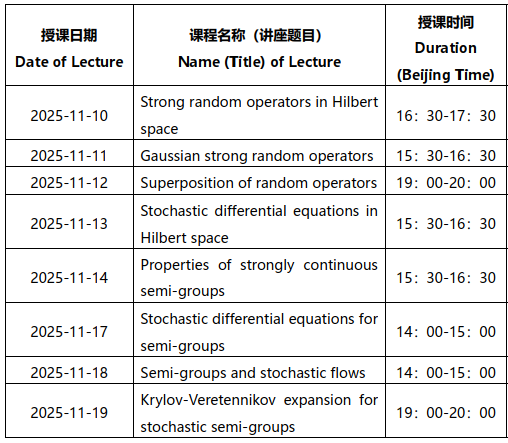
Stochastic semi-groups of random operators
Speaker: Andrey Dorogovtsev(Institute of Mathematics,NAS Ukraine)
Venue: Zoom会议号:814 6465 1975,密码:225776
Abstract: The primary goal of the online mini-school is to illuminate the problems encountered in various branches of stochastic analysis. The strong random linear operators natuarlly arise in the theory of stochastic integration, under investigation of stochastic flows and studying stochastic differential equations. The lectures are suitable for undergraduate students, master's students, young researchers, and everyone interested in this field. The online mini-school provides an excellent platform for creating connections and strengthening international collaborations. The mini-school's online format will allow participants to join remotely from anywhere in the world, providing convenient access to high-quality lectures.
Schedule:
Bio: Andrey Dorogovtsev教授是乌克兰国家科学院通讯院士,乌克兰国家科学院数学所随机过程理论系主任,主要从事概率论及其相关领域研究,是乌克兰概率论研究方向学术领军人物之一。Andrey Dorogovtsev教授是乌克兰与德国、乌克兰与俄罗斯等国家联合项目的乌方负责人。同时,Andrey Dorogovtsev教授是《Theory of Stochastic Processes》、《Ukraine Mathematical Journal》等杂志的编委。
Dirac-Lie systems of differential equations
Speaker: Janusz Grabowski (Polish Academy of Sciences)
Time: October 24, 16:50-17:50
Venue: 吉林大学正新楼209
Abstract: Sophus Lie proved a theorem about nonlinear superposition rules for solutions of some non-autonomous systems of nonlinear ordinary differential equations. These systems can be considered as a generalization of linear systems, as they admit a superposition rule, allowing us to express the general solution of the system by means of a superposition function in terms of a set of fundamental particular solutions, in which the superposition rule is possibly no longer a linear function. Such systems are nowadays called Lie systems. More specific Lie systems have also been studied, e.g., in connection with symplectic or Poisson geometry.
We will discuss Lie systems from a geometric perspective, presenting the fundamental result of Lie in the modern setting, including Dirac structures into the picture. The talk will be illustrated by meny examples.
Bio: Professor Janusz Grabowski is the Head of the Department of Mathematical Physics and Differential Geometry in the Institute of Mathematics, Polish Academy of Sciences. His main interests are differential geometry and mathematical physics. He published fundamental results on Lie algebras of vector fields, diffeomorhism groups, Lie systems, Poisson and Jacobi manifolds, Lie groupoids and algebroids, Lagrangian and Hamiltonian mechanics (including mechanics on contact manifolds), supergeometry, geometry of quantum states and entanglement, etc.
Course on Geometric Mechanics
Speaker: Katarzyna Grabowska (University of Warsaw)
Time: October 23, 10:30-11:30, 13:30-14:30
October 24, 9:00-10:00, 14:30-15:30
Venue: 吉林大学正新楼209
Abstract: According to J.L. Lagrange, the variational description of mechanics ``reduces all the laws of motion of bodies to their equilibrium and thus brings dynamics back into statics''. Since statics is conveniently formulated in the language of differential geometry, we can also view variational calculus as a way to integrate differential geometry into the infinite-dimensional space of trajectories in physical systems. Later, the development of symplectic geometry enabled the application of traditional differential geometry in mechanics once again. This approach was similarly extended to classical field theory through the use of multisymplectic geometry. In this mini-course, we will explore the geometric structures and procedures that comprise Geometric Mechanics. Special attention will be given to mechanical systems that face specific challenges, such as those described by singular Lagrangians or those with nonholonomic constraints. We will discuss mechanics on algebroids and introduce the concept of a Dirac algebroid as a tool for deriving phase equations for systems with nonholonomic constraints, both in the Hamiltonian and Lagrangian settings. The course will be divided into four lectures:
1. Introduction. In the first lecture, we shall review the passage from the variational approach to mechanics to a purely geometrical one. As a result, we shall construct the classical Tulczyjew Triple and examine its applications.
2. Crash course on double vector bundles. The classical Tulczyjew triple is composed of certain double vector bundle morphisms. Before we proceed to the more general setting, we need to understand the concept of a double vector bundle and become familiar with several important examples.
3. Tulczyjew triple in an algebroid setting. During the third lecture, we shall introduce the concept of a general algebroid as a particular double vector bundle morphism and build the appropriate version of a Tulczyjew triple. It will then be used to describe mechanical systems with symmetry and constraints.
4. Dirac structures in nonholonomic mechanics. The last lecture will be devoted to the concept of a linear almost Dirac structure called a Dirac algebroid. It can be used in nonholonomic mechanics as a convenient tool for deriving equations with linear nonholonomic constraints with no restrictions on the Hamiltonian or Lagrangian functions. For example, one can include magnetic or gyroscopic forces in the play.
Bio: Katarzyna Grabowska is a professor in the Department of Mathematical Methods in Physics at the University of Warsaw. She is interested in differential geometric methods in physics and differential geometry in general.
Topology of 4-manifolds
Speaker: Byeorhi Kim Pohang (University of Science and Technology)
Time: October 20-29, 2025
Venue: Zoom ID: 821 6588 8291, Passcode: 3UTCb6
Schedule:
10月20日 13:30-15:00
Title: Topology of 4-manifolds : 1. Basic tools
Content:
This talk will be based primarily on the textbook of Freedman and Quinn. I will explain several key techniques for handling immersions of surfaces. The central tool is the immersion lemma, which is taken axiomatically as a principle for dealing with embeddings of disks. I will also discuss the twisting operation, which is used in the construction of Whitney disks. These Whitney disks are in turn employed to define the Whitney move, one of the fundamental geometric operations in topology across all dimensions.
10月22日 13:00-14:30
Title: Topology of 4-manifolds : 2. Eliminating intersections
Content:
This talk will be based primarily on the textbook of Freedman and Quinn. I will discuss several techniques for eliminating intersections, including the Whitney move, the finger move, and the connected sum. We will also examine the algebraic condition provided by the intersection number, which determines when these geometric operations can be applied. In addition, I will introduce the notion of a transverse sphere, which offers special cases where intersections can be removed.
10月27日 13:30-15:00
Title: Topology of 4-manifolds : 3. Capped surfaces
Content:
This talk will be based primarily on the textbook of Freedman and Quinn. In this talk, we focus on the notion of capped surface, a key tool in the disk embedding theorem. Roughly speaking, a capped surface is obtained from an immersed surface by attaching two–dimensional caps, such as Whitney disks or dual disks. These caps, typically in the form of immersed disks, are attached along the boundary of the original surface (or along the boundary of a Whitney disk) and serve to eliminate intersections or control algebraic intersection numbers.
10月29日 13:30-15:00
Title: Topology of 4-manifolds : 4. Capped grope
Content:
This talk will be based primarily on the textbook of Freedman and Quinn. In this talk, we introduce capped groups, obtained by iterating the construction of capped surfaces. The key property of gropes is that once a certain height has been obtained they can “grow.” It is used to disengage the image of gropes from the fundamental group of the manifold, and in a controlled setting to disengage images from each other. Together with the use of capped surfaces, capped gropes provide a powerful tool to control algebraic intersections while simultaneously resolving geometric intersections.
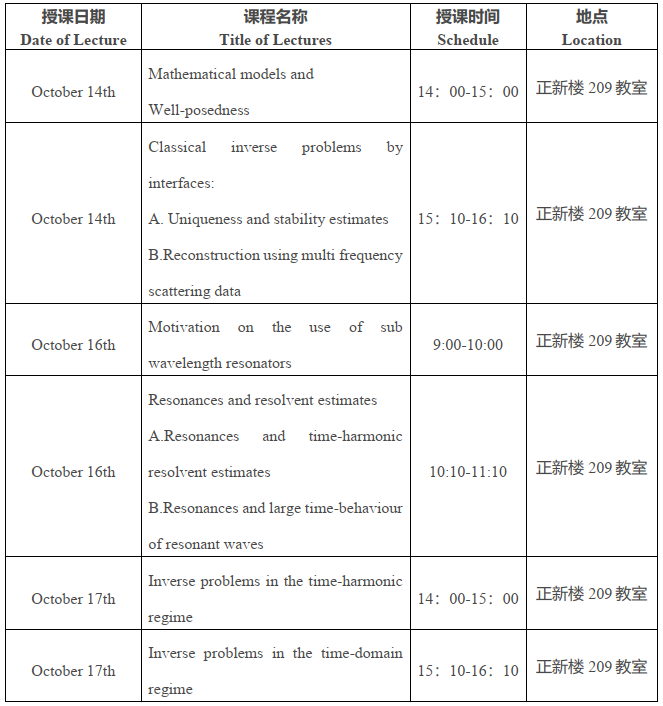
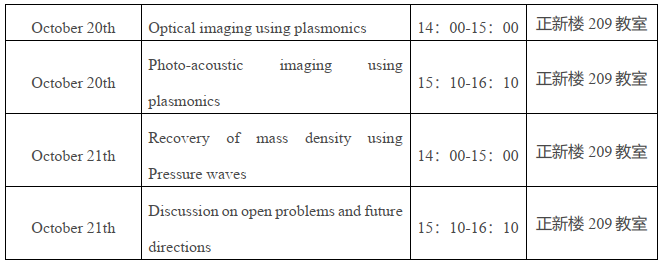
Mathematics of Imaging Modalities Using Resonant Contrast Agents
Speaker: Mourad Sini (Austrian Academy of Sciences)
Time: October 14-21, 2025
Venue: 吉林大学正新楼209教室
Abstract: In this lecture series, we delve into the mathematical modeling, analysis, and practical applications of imaging modalities that leverage resonant contrast agents—an area that has garnered significant attention and rapid development within the applied engineering community. Our focus lies in presenting a systematic, rigorous approach to formulating and solving the family of inverse problems inherent to these advanced imaging techniques, while bridging theoretical insights with real-world imaging scenarios.
Throughout the course, we emphasize the advantages of resonant contrast agents in overcoming longstanding challenges in traditional imaging: they mitigate the non-linearity of inverse problems and improve stability in remote measurements, addressing two major limitations of contrast-agent-free techniques. Finally, we conclude with a discussion of open problems and future directions, inviting participants to engage with unresolved questions—such as refining reconstruction algorithms for complex clustered contrast agents or extending resonant imaging to new modalities—and explore the broader potential of this framework to revolutionize emerging imaging technologies.
Bio: M. Sini got his PhD degree from University of Provence, France, in October 2002. From September 2006, he joined the Radon Institute, of the Austrian Academy of Sciences, where he was tenured since 2011 as a senior fellow (equivalent to university professor) after securing the Habilitation degree from J. Kepler University in 2009. M. Sini was invited to deliver the IAAM Award Lecture (Sweden, August 2019) and an invited plenary speaker in the Applied Inverse Problems (AIP) conference (Grenoble, France, July 2019). He attracted around 2 Mi euro as third-party funding. M. Sini is interested in the analysis of partial differential equations applied to inverse problems, mathematical imaging, mathematical therapy and material theory. By now, he published nearly 100 papers, most of them in top journals, several book chapters and co-edited a book. He is member of the editorial board of several journals including Mathematical Methods in Applied Sciences (Wiley) and Communication on Analysis and Computation (AIMS).
Schedule:
Geometry and Analysis on Higgs bundles
Speaker: Xi Zhang (Nanjing University of Science & Technology)
Time: October 14, 2025, 16:30-17:30
Venue: Zoom ID:904 645 6677, Password:2025
Link: https://zoom.us/j/9046456677?pwd=LJpBPzAw2Sn0MKhb0Qc6QdJ1jEeh7B.1&omn=88293207047
Abstract: Higgs bundle was introduced by Hitchin, it closely related to multiple fields such as non-abelian Hodge correspondence, algebraic geometry, K\"ahler geometry and group representations. In this talk, we introduce our recent works on the existence of canonical metrics on Higgs bundles and their applications. These works are joint with Chao Li, Shiyu Zhang and Chuanjing Zhang.
Bio: 张希,南京理工大学数学与统计学院教授、博士生导师、院长,中国兵工学会应用数学专业委员会主任委员,中国数学会常务理事,江苏省数学会副理事长,中国科学数学编委。主要从事微分几何、几何分析、复几何等方面的研究,在典则度量存在性及相关非线性偏微分方程等方面取得多项研究成果:合作解决Hermitian-Yang-Mills流中的Bando-萧荫堂猜想、给出非凯勒情形数值平坦丛的微分几何刻画、得到带锥奇点凯勒-瑞奇流的收敛性结果,相关工作发表在Adv. Math., Crelle’s Journal, CMP, J.EMS, Math. Ann., PLMS,TAMS等重要数学杂志上。2012年入选中国科学院“百人计划”,2016年获国家自然科学基金杰出青年基金。近五年,主持国家自然科学基金委重点项目、国家重点研发计划专项项目课题等。
Enumerative Geometry of Projective Planes and Their Asymptotic Behavior
Speaker: Shuai Guo (Peking University)
Time: September 16, 2025, 10:00-11:00
Venue: Zoom ID:904 645 6677, Password:2025
Link: https://zoom.us/j/9046456677?pwd=LJpBPzAw2Sn0MKhb0Qc6QdJ1jEeh7B.1&omn=88293207047
Abstract: It is a classical problem in enumerative geometry to count the number of irreducible genus-g, degree-d curves in the projective plane that pass through 3d-1+g generic points. These counts are now known as Gromov-Witten invariants of the complex projective plane.
In this talk, we will first introduce the basic concepts of the moduli space of stable maps and Gromov-Witten invariants, then review the computational methods developed in the existing literature. We will further apply these structural results to the case of the complex projective plane, and investigate the asymptotic behavior of Gromov-Witten invariants for P^2. This is based on a joint work with Gang Tian and Tianhang Xu.
Bio: 郭帅,北京大学博雅特聘教授,数学学院数学物理教研室主任。2006年毕业于清华大学物理系,获基础科学专业学士学位,2011年博士毕业于清华大学数学系,获基础数学博士学位。其主要研究领域为数学物理,尤其聚焦于镜像对称与高亏格计数几何。在这一方向上,成功解决一系列二十多年来长期悬而未解的数学猜想,引起了国际同行的普遍关注。已在包括Annals of Mathematics,Forum of Mathematics, Pi等国际顶尖数学杂志上发表多篇论文。曾入选国家青年拔尖人才支持计划,获国家杰出青年科学基金项目资助,并获求是杰出青年学者奖、教育部青年科学奖、茅以升北京青年科技奖和中国青年科技奖等多项荣誉。
Extensions of solvable Lie and Leibniz algebras
Speaker: Abror Khudoyberdiyev (V.I. Romanovskiy Institute of Mathematics, Uzbekistan)
Time: August 28, 2025 15:00-16:00
Venue: 吉林大学伍卓群楼第六研讨室
Abstract: In this talk, extensions of solvable Lie algebras are considered. The method of central extension is mostly used to obtain a classification of nilpotent algebras. This method was generalized for the solvable Lie algebras by T. Sund in 1979. We investigate extensions of solvable Lie algebras with naturally graded filiform nilradicals. Moreover, we generalize this method for the solvable Leibniz algebras and find extensions of solvable Lie algebras with null-filiform and filiform nilradicals.
Bio: Abror Khudoyberdiyev serves as Deputy Director of the V.I. Romanovskiy Institute of Mathematics and as a Professor at the National University of Uzbekistan. His research interests include non-associative algebras, superalgebras, n-ary algebras, Lie algebras, Leibniz algebras, Zinbiel algebras, evolution algebras, Poisson algebras, the structure theory of algebras, deformations, cohomology, and linear maps. Professor Khudoyberdiyev is the author of more than 70 scientific papers and three books.
An Introduction to Key Cohomology Theories in Differential Geometry
Speaker: Rosa Marchesini (Georg-August-Universität Göttingen)
Time: August 25-27, 2025, 20:00-21:00
Venue: Zoom ID:904 645 6677, Password:2025
Link: https://zoom.us/j/9046456677?pwd=Y2ZoRUhrdWUvR0w0YmVydGY1TVNwQT09&omn=89697485456
Abstract:
Talk 1: An Introduction to Lie Theory.
Lie theory is an active and fruitful area of study in differential geometry, and it is widely used in mathematical physics. After providing an overview of smooth manifolds and vector bundles, we will explain the correspondence between Lie groups and Lie algebras.
Talk 2: An Introduction to de Rham and Chevalley-Eilenberg Cohomology.
Cohomology theories are useful tools for studying some geometric and topological properties of objects in a given category. De Rham cohomology provides information about manifolds, and Chevalley-Eilenberg plays a central role in studying Lie algebras. After defining differential forms of vector spaces and vector bundles, we will introduce de Rham and Chevalley-Eilenberg cohomologies. We will explain some of their properties. We will focus particularly on the homotopy invariance of de Rham cohomology.
Talk 3: An Invitation to Lie Algebroid Cohomology.
Lie groups and Lie algebras are not general enough to describe some physical phenomena. Relaxing their definitions allows for more flexibility. Therefore, we move on to the field of higher Lie theory, in which Lie groupoids and Lie algebroids play a central role in research. Our focus is on Lie algebroid cohomology, also because it allows us to address several types of cohomology theories simultaneously. These include de Rham and Chevalley-Eilenberg cohomology, as well as foliated, Poisson, and equivariant de Rham cohomologies. After introducing Lie algebroids and their cohomology, we will discuss recent research on homotopy for Lie algebroids. These results are a joint work with M. Jotz.
Bio: Rosa Marchesini has completed her bachelor's degree in Mathematics at the University of Turin in Italy. She then studied in the Algant Double Master's Degree Excellence Program at the universities of Milan, Italy, and Bordeaux, France. She is currently a Ph.D. student at the University of Göttingen in Germany. Her advisor is Madeleine Jotz. Starting in October, She will be a postdoc at the University of Würzburg in Germany.
Invariant theory of Hamiltonian mechanics and related numerical analysis
Speaker: Oscar Cosserat (Göttingen Mathematisches Institut)
Time: August 19-21, 2025, 20:00-21:00
Venue: Zoom ID:904 645 6677, Password:2025
Link: https://zoom.us/j/9046456677?pwd=Y2ZoRUhrdWUvR0w0YmVydGY1TVNwQT09&omn=89697485456
Abstract: Hamiltonian systems on Poisson manifolds appear naturally in conservative mechanics as a byproduct of Newton's second law. They provide an efficient formalism to handle symmetries and to tackle stability problems. This is why the question of constructing adapted numerical methods is natural. This lecture is devoted to explain properties of Hamiltonian systems and to develop tools in order to construct numerical integrators for such dynamical systems.
We will first define Poisson manifolds and Hamiltonian systems, and explain their properties through numerous examples. We will then introduce the notion of symplectic groupoid, and illustrate the interest and the power of such an approach to study Hamiltonian systems on Poisson manifolds. In particular, we will use symplectic groupoid theory to construct numerical methods that are adapted to Hamiltonian systems. Finally, we will give examples and illustrations in numerical analysis of those constructions.
Lecture 1: Invariant theory of Hamiltonian mechanics and related numerical analysis I, 20:00-21:00, Aug 19, 2025
Lecture 2: Invariant theory of Hamiltonian mechanics and related numerical analysis I II, 20:00-21:00, Aug 20, 2025
Lecture 3: Invariant theory of Hamiltonian mechanics and related numerical analysis I III, 20:00-21:00, Aug 21, 2025
Bio: Oscar Cosserat is a postdoctoral researcher at the Göttingen Mathematisches Institut, in Germany. He received his PhD in 2023 from the University of La Rochelle, France. His research focuses on the interplay between theoretical mechanics, numerical analysis and differential geometry.
Hopf Galois extensions (quantum principal bundles) and gauge groupoid
Speaker: Xiao Han (Queen Mary University of London)
Time: August 07, 2025, 21:00-22:00
Venue: Zoom ID:904 645 6677, Password:2025
Link: https://zoom.us/j/9046456677?pwd=Y2ZoRUhrdWUvR0w0YmVydGY1TVNwQT09&omn=89697485456
Abstract: I will give a talk on the fundamental aspect of Hopf Galois extensions, which play a role as a “quantum” principal bundle. We know principal bundle offers a beautiful language in the gauge theory, where the connection plays the role of gauge potential. So as one approaches to quantum gauge theory, Hopf Galois extension offers a similar picture. Here I will also introduce the Monopole bundles over Podles sphere as an interesting example. Moreover, I will also introduce quantum gauge groupoids and bisections.
Bio: 韩笑博士2011年毕业于兰州大学理论物理本科,后于德国哥廷根大学获数学硕士学位,2020年于意大利国际高等研究院获数学物理与几何方向博士学位。2020至2021年于波兰科学院数学研究所担任助理教授,2021年至今于伦敦玛丽女王大学作访问研究。韩笑获欧盟“玛丽居里学者计划”资助。其感兴趣的研究方向为Hopf algebras, Hopf algebroids (Groupoids and their Quantization), Noncommutative Geometry, Non-commutative principle bundle (Hopf Galois exension), Mathematical Physics.
Finite-dimensional Lie algebras
Speaker: Maxim Goncharov (Sobolev Institute of Mathematics)
Time: July 23-26, 27-31, 2025, 15:30-16:30
Venue: Zoom ID:814 1002 3263, Password:2025
Link: https://us06web.zoom.us/j/81410023263?pwd=0ysq272PCzQqZjuOoLJTvbwV99Xub2.1
Abstract: In this lecture course, we will focus on the basic theory of finite-dimensional Lie algebras over an algebraically closed field of characteristic 0. We will discuss main notions and constructions (derivations, the Radical, Killing form, and the universal enveloping algebra) and classical results (such as Engel's theorem, Cartan's Criterion, and Weyl's theorem) in the theory of Lie algebras. Also, we will consider some exercises to illustrate the theory and gain practical experience. The minicourse is organized as follows:
1. Definition and basic examples of Lie algebras.
2. Ideals, homomorphisms, automorphisms, and derivations of Lie algebras.
3. Solvability and nilpotency of Lie algebras. Engel's theorem.
4. Jordan-Chevalley decomposition, Cartan's Criterion for Solvability.
5. Killing form, semisimple Lie algebras.
6. Representations and modules of Lie algebras. Schur's Lemma.
7. Weyl's theorem.
8. Universal enveloping algebra. PBW theorem.
Bio: Maxim Goncharov, Ph.D., Senior research fellow in Sobolev Institute of Mathematics, Associate Professor at Novosibirsk State University.
Gröbner-Shirshov basis for associative algebras
Speaker: Vsevolod Gubarev (Sobolev Institute of Mathematics)
Time: July 23-26, 27-31, 2025, 10:30-12:00
Venue: Zoom ID:814 1002 3263, Password:2025
Link: https://us06web.zoom.us/j/81410023263?pwd=0ysq272PCzQqZjuOoLJTvbwV99Xub2.1
Abstract: We will study the Gröbner-Shirshov bases theory for associative algebras with complete proofs and wide applications in (semi)group theory and ring theory. We will also consider computations of Gröbner-Shirshov bases in different computer algebra systems. The minicourse is organized as follows:
1. Free semigroup
2. Defining relations in semigroups and algebras
3. Gröbner-Shirshov basis
4. Rewriting system
5. Composition Lemma
6. Applications in (semi)groups
7. Applications in algebras
8. Computation in computer algebra systems
Bio: Vsevolod Gubarev is a senior researcher in Sobolev Institute of Mathematics and senior teacher in Novosibirsk State University (both in Novosibirsk, Russia). Area of interest: ring theory.
Introduction to Principaloid Bundles
Speaker: Thomas Strobl (University of Lyon)
Time: July 15, 2025 16:30-17:30
Venue: 吉林大学数学楼第五研讨室
Abstract: Standard gauge theories are based on principal G-bundles and associated bundles, where G is a (finite-dimensional) Lie group. However, there are gauge theories that do not fit within this framework, including the Poisson sigma model, gauged standard sigma models with a metric that does not admit isometries, and curved Yang-Mills-Higgs gauge theories. For this purpose we introduce principaloid bundles P, which are based on structure Lie groupoids. These are honest fiber bundles and as such fundamentally different from principal groupoid bundles. We show that ordinary principal bundles, their associated bundles, as well as general fiber bundles are particular examples. We study connections on them, their gauge transformations, and construct the Atiyah groupoid of P, which governs its symmetries. This is joint work with Rafal Suszek.
Bio: Thomas Strobl is a professor in the mathematics department at the University of Lyon. His work as a mathematical physicist is mainly concerned with geometric and algebraic aspects of sigma models and gauge theories. In 1993, during his PhD thesis and together with P. Schaller, he discovered the Poisson Sigma Model; it was used later by M. Kontsevich to obtain his famous quantization formula. In 2015 he and A. Kotov introduced a generalisation of Yang-Mills gauge theories to the Lie algebroid setting. In total, in his career he authored more than 60 scientific articles.
Fundamental groups and category theory
Speaker: Andrey Lazarev (Lancaster University)
Venue: 吉林大学数学楼第五研讨室
Abstract: This course introduces some of the basic notions of category theory such as natural constructions (functors) and equivalence of categories. The category of sets with a group action is studied as an example. This category is then related to the category of covering spaces on a given topological space (this part requires learning or taking on trust some of the results of Minicourse 1). If time permits, an outline of Galois theory as an equivalence of categories will be given.
(1) 14:30-15:30, July 6, 2025, Categories, functors and equivalence of categories
(2) 14:30-15:30, July 7, 2025, The category of sets with a group action. Orbits and stabilizers.
(3) 14:30-15:30, July 9, 2025, Classification of covering spaces as an equivalence of categories.
(4) 14:30-15:30, July 10, 2025, Outline of Galois theory as an equivalence of categories. Analogy with covering spaces.
Bio: Andrey Lazarev,英国兰卡斯特大学教授,从事代数拓扑与同伦论的研究,曾担任 Bull. Lond. Math. Soc.杂志主编,在Adv. Math.、 Proc. Lond. Math. Soc.、 J. Noncommut. Geom.等杂志上发表多篇高水平论文。
On the solvable Poisson algebras
Speaker: Bakhrom Omirov (Institute for Advances Study of Mathematics, Harbin Institute of Technology)
Time: June 26, 2025 15:00-15:50
Venue: 吉林大学数学楼第五研讨室
Abstract: In this talk we present the results on the study of finite-dimensional nilpotent and solvable Poisson algebras. We establish classical results such as Engel’s theorem and Lie’s theorem for Poisson algebras, and examine the role of idempotents in these algebras. The construction of nilpotent and solvable Poisson algebras, exploring the existence of Poisson algebras associated with a fixed Lie algebra, and constructions involving the tensor product and generalized Jacobians will be presented. Furthermore, we show that, under mild restrictions, the solvability and nilpotency of a Poisson algebra are essentially determined by those of the Lie bracket. A criterion for the non-existence of Poisson algebra structures on solvable extensions of nilpotent Lie algebras by a torus will be provided. In particular, we show that complete solvable Lie algebras do not admit a Poisson algebra structure.
Bio: Bakhrom Omirov is a professor at the Harbin Institute of Technology, Institute for Advances Study of Mathematics. He graduated Novosibirsk State University (Russia), got his PhD (2002) and Doctor of Sciences (2006) degrees at Institute of Mathematics of Uzbekistan Academy of Sciences. His research focused on solvable Lie and Leibniz (super)algebras, n-Lie algebras and finite-dimensional Poisson algebras. He published more than 120 publications.
Bakhrom Omirov is a member of The World Academy of Sciences (TWAS) for the advancement of science in developing countries and were awarded by "Top Researcher in Natural Sciences" Scopus Award (2018), Web of Science Awards in the category of "Highly cited author" (2017) and with the highest state prize of the Republic of Uzbekistan in the field of science and technology (2017).
Cosimplicial monoids and deformation theory of tensor categories
Speaker: Michael Batanin (Mathematical Institute, Czech Academy of Sciences)
Time: June 26, 2025 14:00-14:50
Venue: 吉林大学数学楼第5研讨室
Abstract: We introduce a notion of n-commutativity for cosimplicial monoids in a symmetric monoidal category V, where n=0 corresponds to just cosimplicial monoids in V while n=\infty corresponds to commutative cosimplicial monoids. If V has a monoidal model structure we show (under some mild technical conditions) that the totalisation of an n-cosimplicial monoid has a natural E_{n+1}-algebra structure. Our main applications are to the deformation theory of tensor categories and tensor functors. We show that the deformation complex of a tensor functor is a total complex of a 1-commutative cosimplicial monoid and, hence, has an E_2-algebra structure similar to the E_2-structure on Hochschild complex of an associative algebra provided by Deligne's conjecture. We further demonstrate that the deformation complex of a tensor category is the total complex of a 2-commutative cosimplicial monoid and, therefore, is naturally an E_3-algebra. We make these structures very explicit through a language of Delannoy paths and their noncommutative liftings.
Bio: The speaker graduated from Novosibisk State University in 1983. He is currently a Senior Researcher at the Institute of Mathematics of Czech Republic, and a Professor of Charles University in Prague. He is specialising in Algebraic Topology, Category Theory, Operads and related topics.
Generalized Capelli identities
Speaker: Naihuan Jing (North Carolina State University)
Time: June 26, 2025 10:30-12:30
Venue: 吉林大学数学楼第五研讨室
Abstract: The Capelli identity is one of the most important results of classical invariant theory. We will discuss the Capelli identities from different points of view. A new generalization of Capelli identity for immanant will be introduced that generalizes Okounkov's identities. We will also present generalized Turnbull's identities for both symmetric and antisymmetric matrices, as well as the generalized Howe-Umeda-Kostant-Sahi identities for antisymmetric matrices which confirm the conjecture of Caracciolo, Sokal and Sportiello. This is joint work with Jian Zhang.
Bio: 景乃桓,耶鲁大学博士,北卡州立大学终身教授。主要从事无限维李代数、量子群、表示论、代数组合和量子计算方面的研究工作。景乃桓教授在对称函数方面的研究成果被国际上命名为“景氏算子”,在国际主要数学刊物上发表近百篇论文,编辑著作5部。
Fundamental groups and covering spaces
Speaker: Andrey Lazarev (Lancaster University)
Venue: 吉林大学数学楼第五研讨室
Abstract: This course covers the definition and basic properties of homotopy groups of topological spaces, a fundamental notion of algebraic topology. The special role of the first homotopy group (called the fundamental group) is explained. One of the most efficient methods of computing the fundamental group relies on the construction of a universal covering and a theory of covering spaces is developed up to and including their classification. Various concrete examples of computation are given.
(1)10:00-11:00, June 25, 2025,Reminder on homotopy groups, examples. Commutativity of higher homotopy groups.
(2)9:00-10:00, June 26, 2025,Covering spaces and their connection with the fundamental group of the base.
(3)9:00-10:00, June 27, 2025,Computation of the fundamental group using the method of the universal covering. Examples: wedges of circles, tori, the Klein bottle, real projective spaces.
(4)9:00-10:00, June 28, 2025,Classification of covering spaces.
Bio: Andrey Lazarev,英国兰卡斯特大学教授,从事代数拓扑与同伦论的研究,曾担任 Bull. Lond. Math. Soc.杂志主编,在Adv. Math.、 Proc. Lond. Math. Soc.、 J. Noncommut. Geom.等杂志上发表多篇高水平论文。
On double extensions of quasi-Frobenius Lie superalgebras with degenerate center
Speaker: Sofiane Bouarroudj (New York University Abu Dhabi)
Time: June 19, 2025, 21:00-23:00
Venue: Zoom ID:904 645 6677, Password:2024
Link: https://zoom.us/j/9046456677?pwd=Y2ZoRUhrdWUvR0w0YmVydGY1TVNwQT09&omn=89697485456
Abstract: We develop the process of symplectic double extensions for Lie superalgebras with degenerate center. The construction is a superization of a recent work by Fischer, and generalizes our previous work. We provide a standard model for such double extensions, where the symplectic form is either orthosymplectic or periplectic. Additionally, we show that every double extension is naturally equivalent to either of these two standard types of extensions. This is a joint work with Q. Ehret and Y. Maeda.
Bio: Sofiane Bouarroudj is a Professor of Mathematics at New York University Abu Dhabi since 2012, and his mathematical interests include structure and representation theory of nonassociative algebras, with an emphasis on modular Lie superalgebras. He got his BS from University of Constantine, Algeria; MS from Université de Paris VII (Denis Diderot), France; and PhD from Université de Provence (Aix-Marseille I), France. Before joining NYUAD, he held several postdoctoral positions in Belgium, France, Italy, and Japan.
Optimality conditions at infinity for nonsmooth minmax programming problems with applications
Speaker: Do Sang Kim (韩国釜庆大学)
Time: June 11, 2025 15:00-17:00
Venue: 吉林大学数学楼三楼第四研讨室
Abstract: In this talk, we focus on the study of optimality conditions at infinity in non smooth minimax programming problems and their applications. By means of the limiting subdifferential and the normal cone at infinity, we derive necessary and sufficient optimality conditions of the Karush–Kuhn–Tucker type for nonsmooth minimax programming problems with constraints. The obtained results are applied to nonsmooth vector optimization problems and robust minimax optimization ones.
Bio: Do Sang Kim,韩国釜庆大学教授,曾先后在意大利、美国作访问学者,多年来致力于多目标最优化,广义凸分析,变分分析等方向的研究,至今累计发表Mathematical Programming,Mathematics of Operations Research, Journal of Optimization Theory and Applications等优化领域高水平论文100余篇,现担任 Journal of Nonlinear and Convex Analysis 等学术期刊编委,曾先后主持韩国 BK21(21 世纪 Brain Korea), BK21+(21 世纪 Brain Korea Program of Leading Universities & Students)等团体学术项目以及韩国研究财团的个人研究项目多项。因众多突破性的研究成果,Kim教授先后获得釜山科学技术奖,韩国数学会特别功劳奖/教育奖等多项奖项。
Subdifferentials at infinity and some applications
Speaker: Nguyen Van Tuyen (越南河内第二师范大学)
Time: May 27, 2025 16:00-17:00
Venue: 吉林大学数学楼三楼天元研讨室四
Abstract: In this talk, we introduce some properties of the limiting and the singular subdifferentials at infinity for extended real value functions, which were recently proposed by Kim, Nguyen and Pham. We then present its applications in studying the existence of error bounds, optimality conditions, the weak sharp minima property at infinity and the solution stability under linear perturbation.
Bio: Nguyen Van Tuyen,河内第二师范大学教授,博士生导师,长期从事向量优化理论、二阶变分分析理论等研究工作,在Mathematical Programming, SIAM Journal on Control and Optimization, Journal of Global Optimization, Journal of Optimization Theory and Applications等优化顶级期刊发表学术论文30余篇。现任河内第二师范大学数学学院副院长,国际SCI期刊Optimization编委。
Local minimizers versus infima at infinity
Speaker: Tien-Son Pham (越南Dalat University)
Time: May 27, 2025 15:00-16:00
Venue: 吉林大学数学楼三楼天元研讨室四
Abstract: Let $f \colon \mathbb{R}^n \to \mathbb{R} \cup \{\infty\}$ be a lower semicontinuous and semialgebraic function. In this talk, we give a complete characterization of the infimum value at infinity of $f$ and show some relationships between {\L}ojasiewicz exponents at infinity of $f$ for this value.
Bio: Tien-Son Pham,越南Dalat University教授,博士生导师,长期从事奇异理论、半代数优化、变分分析等研究工作,在Mathematical Programming, SIAM Journal on Optimization, Mathematics of Operations Research等优化顶级期刊发表学术论文70余篇,出版学术专著1部。2020年获越南科技部颁发的Ta Quang Buu奖,并入选2021年度“亚洲百位杰出科学家”榜单(该榜单由亚洲科学家杂志自2016年起每年评选,表彰在科研领域取得重大突破或获得国家级/国际奖项的科学家)。现任越南高等数学研究所科学理事会(Scientific Council)成员。
On solving fractional SOS convex moment problems
Speaker: Gue Myung Lee (韩国釜庆大学)
Time: May 27, 2025 14:00-15:00
Venue: 吉林大学数学楼三楼天元研讨室四
Abstract: Recently, many authors have studied fractional optimization problems and moment problems. The moment problems have been well known and very useful for many real problems. In this talk, we consider a fractional moment problem involving SOS convex polynomials, and obtain a linear semidefinite optimization problem by using the Lagrangian dual problem of the fractional moment problem. We show that we can obtain the solutions of the fractional moment problem from the ones of the linear semidefinite optimization problem.
Bio: Gue Myung Lee,韩国釜庆大学应用数学专业荣休教授,基础科学研究所客座研究员。曾先后多次在日本、中国、越南、美国、澳大利亚、印度、泰国等国家作访问学者。长期从事变分分析、多目标优化、多项式优化、非光滑优化、凸优化等研究工作,取得了一系列标志性的研究成果,在Mathematical Programmng、SIAM Journal on Optimization等学术期刊论文200余篇,并出版学术专著1部,曾获韩国数学会最佳论文奖等。
An invitation to multi-symplectic geometry
Speaker: Leonid Ryvkin (Université Claude Bernard Lyon 1, Villeurbanne, France)
Venue: Zoom ID:904 645 6677, Password:2024
Link: https://zoom.us/j/9046456677?pwd=Y2ZoRUhrdWUvR0w0YmVydGY1TVNwQT09&omn=89697485456
Abstract: In this series of talks we are going to give an introduction to multi-symplectic geometry, a generalization of symplectic geometry which was originally developed to describe classical field theories in a covariant and finite-dimensional way. We will discuss the following topics:
* Darboux type theorems (What do multi-symplectic manifolds look like?)
* momentum geometry (from an $L_\infty$-algebra perspective)
* Reduction (from an algebraic viewpoint)
Lecture 1: An invitation to multi-symplectic geometry I, 20:00-21:30, May 26, 2025
Lecture 2: An invitation to multi-symplectic geometry II, 20:00-21:30, May 27, 2025
Lecture 3: An invitation to multi-symplectic geometry III, 20:00-21:30, May 28, 2025
Lecture 4: An invitation to multi-symplectic geometry IV, 20:00-21:30, May 29, 2025
Bio: Leonid Ryvkin completed his Phd on multisymplectic geometry at the Ruhr-University of Bochum in 2018. After postdoctoral stays in Paris and Göttingen, he is now a Maitre de Conférences at the University Claude-Bernard Lyon 1. His primary interest is the application of higher structures to problems in differential geometry and mathematical physics.
Numerical Homological Regularities
Speaker: 吴泉水 (复旦大学)
Time: May 24, 2025 14:00-15:00
Venue: 吉林大学数学楼第5研讨室
Abstract: Inspired by the studies in algebraic geometry and commutative algebra, Jorgensen defined Castelunovo-Mumford regularities for graded modules over noncommutative noetherian connected graded algebras. I will survey the new developments and our recent work on the numerical homological regularities with Bojuan Yi.
Bio: 吴泉水,复旦大学数学科学院教授、博士生导师;长期从事非交换代数的科学研究和人才培养工作,研究领域包括非交换环论、非交换代数几何、Hopf代数/量子群的同调理论等,在国内外著名学术刊物包括Duke Math .J. 和Trans. AMS等发表学术论文50余篇,曾解决所在领域的几个公开问题或猜想,在相关研究领域做出重要贡献。
Partial groups, Partial categories, and applications to Hall algebras
Speaker: Zongzhu Lin (Kansas State University, USA)
Time: May 15, 2025 10:30-12:30
Venue: 吉林大学数学楼第5研讨室
Abstract: Alperin studied the fusion properties of subgroups of a Sylow p-subgroup of finite group in 1967, which lead to later development of fusion systems. Fusion system is regarded as a local group theory. In the attempt to characterize fusion systems in terms of homotopy theory, the concept of localities and partial groups were introduced. Around the same time Kriz and May also introduced partial algebras in an attempt to formalize the intersection multiplication of motives. It turns out that both concepts are pretty much the same in categorical setting, where multiplications need not to be defined as they should. To do so one has to define the concepts of domains in both settings. The concept of partial categories can be defined in a similar fashion. Partial categories can be used as a framework to bridge several different mathematical structures. In this talk, I will focus on realizing Hall algebras of an abelian category as the Grothendieck ring of a partial category attached to the abelian category. This is an attempt to investigate the relations between Hall algebras and cohomology theory of simplicial sets.
Bio: 林宗柱,美国堪萨斯州立大学终身教授,博士生导师,主要从事表示论、代数群以及量子群等方面的研究,在 Invent. Math.,Adv. Math., Trans. Amer. Math. Soc., CMP 和J. Algebra 等重要学术期刊上发表论文数十篇,标志性成果包括林-Nakano定理,出版学术著作五部。
Diffeology and Lie's third theorem
Speaker: David Miyamoto (Max Planck Institute for Mathematics, in Bonn, Germany)
Venue: Zoom ID:904 645 6677, Password:2024
Link: https://zoom.us/j/9046456677?pwd=Y2ZoRUhrdWUvR0w0YmVydGY1TVNwQT09&omn=89697485456
Abstract: Lie's third theorem is the result that every finite-dimensional Lie algebra integrates to a Lie group. Its two possible generalizations fail: not every Lie algebroid integrates to a Lie groupoid, and not every Banach Lie algebra integrates to a Banach Lie group. In this series of talks, we will show how diffeology, a category of generalized smooth spaces introduced by Souriau in the 1980s, can address this shortcoming.
In the first talk, we will introduce diffeology, with a focus on examples and relations to other smooth structures (orbifolds, infinite-dimensional manifolds, manifolds with boundary). This introduction will extend to the second talk, where we will discuss diffeology's role in the theory of Lie groupoids and singular foliations. Finally, in the third talk, we will present the machinery needed to diffeologically integrate certain Banach Lie algebras which admit no classical integration, and remark on the case for Lie algebroids.
Lecture 1: Diffeology and Lie's third theorem I, 20:00-21:00, May 13, 2025
Lecture 2: Diffeology and Lie's third theorem II, 20:00-21:00, May 14, 2025
Lecture 3: Diffeology and Lie's third theorem III, 20:00-21:00, May 15, 2025
Bio: David Miyamoto is a postdoctoral researcher at the Max Planck Institute for Mathematics, in Bonn, Germany. He received his PhD from the University of Toronto, Canada, in 2023. His research focuses on the interplay between higher structures in differential geometry and diffeology.
On reflections to set-theoretic solutions of the Yang-Baxter equation
Speaker: Paola Stefanelli (University of Salento)
Time: April 10, 2025, 21:00-23:00
Venue: Zoom ID:904 645 6677, Password:2024
Link: https://zoom.us/j/9046456677?pwd=Y2ZoRUhrdWUvR0w0YmVydGY1TVNwQT09&omn=89697485456
Abstract: The Yang-Baxter equation (YBE) is a fundamental equation of mathematical physics that has been extensively studied in the last few years. Alongside it, the reflection equation serves as a significant tool in the theory of quantum groups and integrable systems, which was first investigated in 1984 by Cherednik. In 2013, Caudrelier, Crampé, and Zhang formulated the set-theoretic version of the YBE, and, later on, some new results were obtained, mainly concerning involutive and non-degenerate solutions.
This talk aims to present a strategy for determining reflections to left non-degenerate set-theoretic solutions (X, r) of the YBE as provided in a joint work with A. Albano and M. Mazzotta, and obtained by examining the behavior of these solutions with their derived solutions or, equivalently, with (left) self-distributive structures associated with them. Our approach is strongly motivated by a recent description of left non-degenerate solutions (X, r) in terms of Drinfel’d twist, namely, a family of automorphisms of the shelf associated with (X, r), which is obtained in a joint paper with A. Doikou and B. Rybołowicz.
Bio: Paola Stefanelli is currently a Tenured Assistant Professor at the University of Salento, where she earned her PhD in 2015 under the supervision of Prof. Francesco Catino. Her research focuses on the interaction between set-theoretical solutions to the Yang-Baxter equation and various algebraic structures, such as skew braces, cycle sets, racks, and their generalizations. She pays particular attention to the constructive aspects of these solutions and, more recently, to their associated reflections. Additionally, she is interested in studying set-theoretical solutions to the pentagon equation for specific classes of semigroups. Another area of her research involves describing the regular subgroups of the affine group of a vector space.
Weak braces and solutions of the Yang-Baxter equation
Speaker: Marzia MAZZOTTA (University of Salento)
Time: April 3, 2025, 21:00-23:00
Venue: Zoom ID:904 645 6677, Password:2024
Link: https://zoom.us/j/9046456677?pwd=Y2ZoRUhrdWUvR0w0YmVydGY1TVNwQT09&omn=89697485456
Abstract: Weak braces are algebraic structures that include skew braces and give rise to set-theoretic solutions of the Yang-Baxter equation, which are close to being bijective and non-degenerate. We show that a class of weak braces is obtained as a strong semilattice of certain specific skew braces. Consequently, also their associated solution is the strong semilattice of the bijective non-degenerate solutions associated with each of these skew braces. The talk is based on a joint work in collaboration with Francesco Catino and Paola Stefanelli.
Bio: Marzia received her Master’s degree from the University of Salento in 2016 and her Ph.D. degree from the same university in 2020, under the supervision of Prof. Francesco Catino. Her Ph.D. thesis focuses on the Pentagon equation, above all set-theoretic solutions defined on specific semigroups. She has been a PostDoc at the University of Salento since 2020. Marzia’s research is centered on algebraic structures connected to the Yang-Baxter equation, such as braces and their generalizations. Moreover, she also continues to investigate special classes of set-theoretic solutions to the Pentagon equation.
Yang-Baxter and Zamolodchikov tetrahedron maps
Speaker: Sotiris Konstantinou-Rizos (P.G. Demidov Yaroslavl State University, Russia)
Time: March 20, 2025, 21:00-23:00
Venue: Zoom ID:904 645 6677, Password:2024
Link: https://zoom.us/j/9046456677?pwd=Y2ZoRUhrdWUvR0w0YmVydGY1TVNwQT09&omn=89697485456
Abstract: In this talk, I will give an introduction to the theory of Yang-Baxter and tetrahedron maps, which are set-theoretical solutions to the Yang-Baxter and the Zamolodchikov tetrahedron equation, respectively. I will explain the relation between them, as well as their relations to matrix refactorisation problems and discrete integrable systems. Then, I will briefly review some generalisations of the Yang-Baxter and Zamolodchikov tetrahedron equation.
Bio: Sotiris Konstantinou-Rizos is working as an Associate Professor at the P.G. Demidov Yaroslavl State University, Russia. He holds a PhD degree from the University of Leeds, the UK, while his main studies (BSc. and MSc.) took place at the University of Patras, Greece. His main research interests are discrete integrable systems, Darboux-Bäcklund transformations, soliton theory and n-simplex equations.
Tanaka prolongation procedure, Kantor algebras, and (homotopy) Leibniz structures
Speaker: Alexei Kotov (University of Hradec Králové)
Time: March 13, 2025, 21:00-23:00
Venue: Zoom ID:904 645 6677, Password:2024
Link: https://zoom.us/j/9046456677?pwd=Y2ZoRUhrdWUvR0w0YmVydGY1TVNwQT09&omn=89697485456
Abstract: In the first part of this lecture a brief introduction to Tanaka's theory of prolongation of non-positively graded Lie algebras will be given. This procedure will then be applied to a free Lie superalgebra. It will be shown that the resulting graded Lie superalgebra contains complete information about Leibniz brackets. At the end of the lecture, if time permits, the lecturer will explain the connection between the structures discussed and functional calculus on path spaces.
Bio: Alexei Kotov is a professor in the University of Hradec Králové (UHK),Czechia. His research interests include super- and graded geometry, special Riemannian geometry, Lie algebroids and groupoids, geometry of PDEs, non-linear sigma models.
A friendly introduction to skew braces and their connections with the Yang-Baxter equation
Speaker: Sin Yi Tsang (Ochanomizu University)
Time: March 6, 2025, 20:00-22:00
Venue: Zoom ID:904 645 6677, Password:2024
Link: https://zoom.us/j/9046456677?pwd=Y2ZoRUhrdWUvR0w0YmVydGY1TVNwQT09&omn=89697485456
Abstract: Skew brace is an algebraic structure that arose out of the study of set-theoretic solutions to the Yang-Baxter equation. In this talk, I will start with the definition and basic examples of skew braces, and then I will explain some connections between skew braces and solutions to the Yang-Baxter equation. I will also discuss some research directions in the study of skew braces from the algebraic point of view.
Bio: Sin Yi Tsang has been a faculty member at Ochanomizu University since April 2021. She received her Ph.D. from the University of California, Santa Barbara in 2016. Before coming to Japan, she was a research fellow at Sun Yat-Sen University, Zhuhai (2018~2020), and a postdoctoral fellow at the Yau Mathematical Sciences Center at Tsinghua University (2016~2018). Other than skew braces, she is also interested in Hopf-Galois structures and regular subgroups of the holomorph.
Integrable Birkhoff billiards inside cones
Speaker: Andrey Mironov (Sobolev Institute of Mathematics)
Time: February 21, 2025 10:30-12:30
Venue: 吉林大学数学楼第五研讨室
Abstract: The classical Birkhoff conjecture states that if the plane billiards inside a closed smooth convex curve is integrable then the curve is an ellipse. In higher dimensions, all known integrable billiards are inside billiard tables consisting of pieces of quadrics. We study Birkhoff billiards in convex cones in Rn and prove that billiards in any C3-smooth convex cone are integrable. This provides the first examples of integrable billiard tables in Rn not related to quadrics.
Bio: Professor Andrey Mironov is the acting director of Sobolev Institute of Mathematics, Corresponding member of Russian Academy of Sciences. His research interest includes Integrable Systems, Geometry, Mathematical Physics and Dynamical Systems.
Lie Groupoids and Related Structures
Speaker: Matias del Hoyo (Universidade Federal Fluminense)
Time: February 18,19,20, 2025 10:00-11:00
Venue: 吉林大学数学楼第五研讨室
Abstract:
Talk 1: Lie Groupoids
Abstract: Lie groupoids generalize Lie groups and can be seen as structures on manifolds that encode both internal and external symmetries. Over the last few decades, their theory has significantly evolved, driven by connections to Poisson geometry, non-commutative geometry, and mathematical physics. In this talk, I will provide an overview of Lie groupoids, including basic definitions, key examples, and constructions. I will also discuss the Linearization Theorem and some of its applications, with a particular focus on the theory of Riemannian metrics.
Talk 2: Lie Algebroids and Differentiable Stacks
Abstract: The infinitesimal geometry of a Lie groupoid is captured by its Lie algebroid, a structure that generalizes regular foliations and Lie algebra bundles. Not every abstract Lie algebroid can be integrated, and topological obstructions can be explicitly computed. The transverse geometry of a Lie groupoid is represented by its orbit stack, a structure generalizing manifolds and orbifolds. Two groupoids yield the same stack if and only if they are Morita equivalent, and many invariants and constructions are Morita invariant. I will review these constructions, highlight key results, and discuss my contributions to the field.
Talk 3: Higher Lie Groupoids
Abstract: Higher Lie groupoids arise from the simplicial approach to higher category theory. Notable examples include the global counterparts of Courant algebroids in Poisson Geometry. Just as Lie groupoids relate to Lie algebroids and stacks, higher Lie groupoids connect with differential graded manifolds and higher stacks. However, these theories are still in their early stages, with foundational questions remaining unanswered. In this talk, I will introduce the theory of higher Lie groupoids, present my recent work in the area, and discuss some open problems.
Bio: Prof. Matias del Hoyo has been a faculty member at the Universidade Federal Fluminense (Niterói, Brazil) since 2016. He earned his Ph.D. in Mathematics from the Universidad de Buenos Aires (Argentina) in 2010 and conducted postdoctoral research at Instituto Superior Técnico (Lisbon, Portugal) and Utrecht University (Netherlands) from 2011 to 2013. He also served as a Visiting Professor at IMPA (Rio de Janeiro, Brazil) from 2014 to 2016 and at the Center de Recerca Matemàtica (Barcelona, Spain) in 2019. His research focuses on Lie groupoids, Lie algebroids, and differentiable stacks, with applications in Poisson Geometry.
Products of Kirillov-Reshetikhin modules and maximal green sequences
Speaker: Gleb Koshevoy (Institute for Information Transmission Problems of the Russian Academy of Sciences)
Time: 20:30-22:30, Jan 14, 2025
Venue: ZOOM ID:904 645 6677, Password:2024
Link: https://zoom.us/j/9046456677?pwd=Y2ZoRUhrdWUvR0w0YmVydGY1TVNwQT09&omn=89697485456
Abstract: We show that a $q$-character of a Kirillov-Reshetikhin module (KR-modules) for untwisted quantum affine algebras of simply laced types $A_n^{(1)}$, $D_n^{(1)}$, $E_6^{(1)}$, $E_7^{(1)}$, $E_8^{(1)}$ might be obtained from a specific cluster variable of a seed obtained by applying a maximal green sequence to the initial (infinite) quiver of the Hernandez-Leclerc cluster algebra. For a collection of KR-modules with nested supports, we show an explicit construction of a cluster seed, which has cluster variables corresponding to the $q$-characters of KR-modules of such a collection. We prove that the product of KR-modules of such a collection is a simple module. We also construct cluster seeds with cluster variables corresponding to $q$-characters of KR-modules of some non-nested collections. We make a conjecture that tensor products of KR-modules for such non-nested collections are simple. We show that the cluster Donaldson-Thomas transformations for double Bruhat cells for $ADE$ types can be computed using $q$-characters of KR-modules. This is joint work with Y. Kanakubo and T. Nakashima.
Bio: Gleb Koshevoy is a chief researcher at the Institute for Information Transmission Problems of the Russian Academy of Sciences. His current research interests are algebraic combinatorics and combinatorics of cluster algebras. His main results include: 1) The creation of the theory of discrete convexity in 2003 (with Vladimir Danilov); 2) an almost purely combinatorial solution to the Horn problem on the spectra of a sum of Hermitian matrices in 2003 (with V. Danilov); 3) Local characterization of Kashiwara crystals for simply and doubly laced types in 2009 (with V. Danilov and A. Karzanov) 4) Affirmative answer to the Leclair-Zelevinsky conjecture on the purity of weakly separated sets in 2011 (with V. Danilov and A. Karzanov) and proposed various generalizations of this conjecture 5) Proposal of polynomial-time algorithms for subtraction-free computations of Schur functions and their various generalizations in 2014 (with S. Fomin and D. Grigoriev).
Conformal algebras and their place in the Algebra Universe
Speaker: Pavel Kolesnikov (Sobolev Institute of Mathematics)
Time: 18:00-19:30, Jan 14, 17, 21, 24, Feb 4 and Feb 7., 2025
Venue: ZOOM ID:904 645 6677, Password:2024
Link: https://zoom.us/j/9046456677?pwd=Y2ZoRUhrdWUvR0w0YmVydGY1TVNwQT09&omn=89697485456
Abstract: Conformal algebras are relatively new area of algebraic research based on some structures emerged in mathematical physics. We will observe various equivalent approaches to the definition of conformal algebras and review main results in structure theory and combinatorial techniques in this field. Prerequisites include just associative algebras and their representations, a knowledge on the basics of non-associative algebras and operads is welcome but not necessary.
Bio: Pavel Kolesnikov is a research member of the Sobolev Institute of Mathematics and a professor of Novosibirsk State University. He specializes in the study of non-associative structures emerging in contemporary mathematics, like Rota-Baxter algebras, dendriform algebras, conformal and vertex algebras, etc.
Global bases and canonical bases of quantum Borcherds-Bozec algebras
Speaker: 樊赵兵 (哈尔滨工程大学)
Time: January 3, 2025 16:30-18:30
Venue: 吉林大学数学楼第5研讨室
Abstract: By using new Kashiwara operators, we construct global bases for quantum Borcherds-Bozec algebra. Moreover, we introduce the primitive canonical bases, and prove it coincides with global bases. This is a joint work with Han, Kang and Kim.
Bio: 樊赵兵,哈尔滨工程大学教授,博士生导师,国家级高层次领军人才。研究方向:几何表示论、量子群、Hall代数、Schur-Weyl对偶、Character Sheaves。在Memoris of AMS,Comm. Math. Physics,Transection of AMS,IMRN等国际知名杂志发表学术论文多篇。主持国家自然科学基金面上项目、黑龙江省杰青等项目多项。
K-theory
Speaker: Thomas Schick (University of Göttingen)
Time: December 13, 2024 9:00-10:00
December 14, 2024 9:00-10:00
December 14, 2024 10:10-11:10
December 15, 2024 9:00-10:00
Venue: 吉林大学正新楼209
Abstract: We introduce the K-theory groups of a C∗-algebra and explain its basic properties. In a nutshell, the group K0(A) classifies A-modules (finitely generated projective) and K1(A) classifies automorphisms of the trivial modules. These come up in numerous situations, and at the same time provide information about the structure of the algebra A. We give a glimpse at computation tools and at first applications.
Plan:
• Long exact sequence of an extension
• Matrix and compact operator stability
• Product structure
• Bott periodicity
• Sample calculations (Calkin index sequence)
• A glimpse at the Elliot classification program
Bio: Thomas Schick is a professor of Mathematics at Mathematisches Institut of Universität Göttingen . His Research areas include Topology and Geometry, Geometry and Analysis, K-Theory of C*-algebras, index theory. He was the Managing Editor der Mathematische Annalen (bis April 2022). Now he is Head of the Scientific Advisory Board of Mathematischen Forschungsinstituts Oberwolfach (MFO), Editor of Annales Mathematiques Blaise Pascal, Journal of Homotopy and related structures, and Bulletin of the Iranian Mathematical Society.
Noncommutative Poisson structure and invariants of matrices
Speaker: Farkhod Eshmatov (New Uzbekistan University)
Time: December 5, 2024 16:20-18:20
Venue: 吉林大学数学楼第五研讨室
Abstract: We introduce a novel approach that employs techniques from noncommutative Poisson geometry to comprehend the algebra of invariants of two~$n\times n$ matrices. We entirely solve the open problem of computing the algebra of invariants of two $4 \times 4$ matrices. As an application, we derive the complete description of the invariant commuting variety of $4 \times 4$ matrices and the fourth Calogero-Moser space. Joint work with X.García-Martínez and R.Turdibaev.
Bio: Professor Farkhod Eshmatov is the director of department of Mathematics in New Uzbekistan University, mainly works on noncommutative algebraic geometry and mathematical physics.
Modern problems in Stochastic Processes
Speaker: Andrey Dorogovtsev (Institute of Mathematics,NAS Ukraine)
Venue: ZOOM ID:820 0150 4934, Password:748893
Abstract: The primary goal of the online mini-school is to illuminate the modern problems encountered in various branches of stochastic processes theory. Through a series of comprehensive lectures, we aim to explore contemporary research and applications within this field. The lectures are suitable for undergraduate students, master's students, young researchers, and everyone interested in this field. The online mini-school provides an excellent platform for creating connections and strengthening international collaborations. The mini-school's online format will allow participants to join remotely from anywhere in the world, providing convenient access to high-quality lectures.
Schedule:

Set-theoretic Yang-Baxter equation, twists & quandle Hopf algebras
Speaker: Anastasia Doikou (Heriot-Watt University)
Time: November 21, 2024 20:30-22:30
Venue: ZOOM ID:904 645 6677, Password:2024
Link: https://zoom.us/j/9046456677?pwd=Y2ZoRUhrdWUvR0w0YmVydGY1TVNwQT09&omn=89697485456
Abstract: The theory of the set-theoretic Yang-Baxter equation is established from a purely algebraic point of view. The derivation of solutions of the braid equation via certain self-distributive structures called racks and quandles is reviewed. Generic, non-involutive set-theoretic solutions of the braid equation are then obtained from rack solutions by a suitable Drinfl'd twist, whereas all involutive solutions are obtained from the flip map via a twist. The universal algebras associated to both rack and generic set-theoretic solutions are also studied and the corresponding universal R-matrices are derived.
Bio: Anastasia Doikou is a Professor of Mathematics at Heriot-Watt University in Edinburgh. She studied physics as an undergraduate at National & Kapodistrian University of Athens and she obtained her PhD in theoretical and mathematical physics from University of Miami in 1999. Between 1999 and 2007 she held postdoctoral positions at Durham University, University of York (EPSRC Fellow), LAPTH-Annecy and University of Bologna. She was assistant professor at University of Patras in Greece before joining Heriot-Watt University in 2013.
Reflection vectors, monodromy data and Dubrovin conjecture
Speaker: John Alexander Cruz Morales (Universidad Nacional de Colombia)
Time: November 13, 2024 16:00-18:00
Venue: 吉林大学数学楼第五研讨室
Abstract: Using the notion of reflection vectors (which only depends on the second structure connection) I will show how to get explicitly the Stokes and central connection matrices for a semisimple Frobenius manifold. In the case of quantum cohomology, I will discuss some implications for the so-called Dubrovin conjecture which relates the quantum cohomology of a (Fano) manifold with its bounded derived category of coherent sheaves. This is a joint work with Todor Milanov.
Bio: John Alexander Cruz Morales is an associate professor at Universidad Nacional de Colombia. He is mainly interested in mirror symmetry and related topics such as derived categories, integrable systems and representation theory.
Deformations of Symplectic Foliations
Speaker: Alfonso Giuseppe TORTORELLA (University of Salerno)
Time: November 07, 2024 20:00-21:00
Venue: ZOOM ID:904 645 6677, Password:2024
Link: https://zoom.us/j/9046456677?pwd=Y2ZoRUhrdWUvR0w0YmVydGY1TVNwQT09&omn=89697485456
Abstract: In this talk, based on joint work with Stephane Geudens and Marco Zambon, we develop the deformation theory of symplectic foliations, i.e. regular foliations equipped with a leafwise symplectic form. The main result is that each symplectic foliation is attached with a cubic L∞algebra controlling its deformation problem. Indeed, we establish a one-to-one correspondence between the small deformations of a given symplectic foliation and the Maurer–Cartan elements of the associated L∞ algebra. Further, we prove that, under this one-to-one correspondence, the equivalence by isotopies of symplectic foliations agrees with the gauge equivalence of Maurer–Cartan elements. Finally, we show that the infinitesimal deformations of symplectic foliations can be obstructed.
Bio: Alfonso Giuseppe TORTORELLA received his PhD from the University of Florence in 2017, and is currently an Assistant Professor of Geometry at the University of Salerno. His research focuses on the geometry of Poisson and related structures, and studies mainly deformation problems in Poisson geometry.
Desingularizing singular symplectic structures
Speaker: Eva Miranda (Polytechnic University of Catalonia)
Time: October 18, 2024 20:00-22:00
Venue: ZOOM ID:904 645 6677, Password:2024
Link: https://zoom.us/j/9046456677?pwd=Y2ZoRUhrdWUvR0w0YmVydGY1TVNwQT09&omn=89697485456
Abstract: The exploration of symplectic structures on manifolds with boundaries has naturally led to the identification of a “simple” class of Poisson manifolds. These manifolds are symplectic away from a critical hypersurface, but degenerate along this hypersurface. In the literature, they are referred to as b-symplectic or log-symplectic manifolds. They arise in the context of the space of geodesics of the Lorenz plane and serve as a natural phase space for problems in celestial mechanics such as the restricted 3-body problem. Geometrically, these manifolds can be described as open symplectic manifolds endowed with a cosymplectic structure on the open ends.
The technique of "deblogging" or desingularization associates a family of symplectic structures to singular symplectic structures with even exponent (known as b^{2k}-symplectic structures), and a family of folded symplectic structures for odd exponent (b^{2k+1}-symplectic structures). This method has good convergence properties and generalizes to its odd-dimensional counterpart, contact geometry. In this way, the desingularization technique puts under the same umbrella various geometries, such as symplectic, folded-symplectic, contact, and Poisson geometry.
The desingularization kit has a broad range of applications, such as the construction of action-angle coordinates for integrable systems, KAM theory, quantization, and counting periodic orbits.
Bio: Eva Miranda is Chair in Geometry and Topology in the Department of Mathematics at the Polytechnic University of Catalonia, and a member of CRM. She has been a visiting professor at the Paris Observatory, MIT, the University of Toulouse, and the University of Paris 7, and she was an honorary professor at CSIC and an Affiliate Researcher at the Paris Observatory. Miranda is the director of the Geometry and Dynamical Systems Laboratory at UPC and the leader of the Geometry of Manifolds and Applications research group at UPC.
Miranda has been awarded two consecutive ICREA Academia prizes (in 2016 and 2021), a Chair of Excellence from the Paris Mathematical Sciences Foundation in 2017-2018, a Bessel Award from the Humboldt Foundation in 2022, and the François Deruyts Prize in 2022. She was invited speaker at the 8ECM. She was named Hardy Lecturer 2023 by the London Mathematical Society and Nachdiplom Lecturer 2025 by ETHZ. In 2024, she was appointed Gauss Professor by the University of Göttingen.
A post-group theoretic perspective on the operator-valued S-transform in free probability
Speaker: Kurusch Ebrahimi-Fard (Norwegian University of Science and Technology)
Time: October 10, 2024 20:00-22:00
Venue: ZOOM ID:904 645 6677, Password:2024
Link: https://zoom.us/j/9046456677?pwd=Y2ZoRUhrdWUvR0w0YmVydGY1TVNwQT09&omn=89697485456
Abstract: We discuss the algebraic structure underlying Voiculescu's S-transform in operator-valued free probability. It is shown how its twisted factorisation property gives rise to post-groups, crossed morphisms, as well as pre- and post-Lie algebras. Based on joint work with T. Ringeard (arXiv:2402.16450).
Bio: Kurusch Ebrahimi-Fard earned his Ph.D. in Theoretical Physics from the University of Bonn under the supervision of D. Kreimer and R. Flume. He also hold a Maîtrise de Mathématiques from Université Joseph Fourier in Grenoble, France. His past academic roles include postdoctoral positions at the Institut des Hautes Études Scientifiques (IHES, Bures-sur-Yvette, France), the Max Planck Institute for Mathematics (MPIM, Bonn, Germany), Universidad de Zaragoza (Zaragoza, Spain), and Instituto de Ciencias Matemáticas (ICMAT, Madrid, Spain), as well as an associate professorship (Maître de Conférences) at Université de Haute-Alsace (Mulhouse, France). Since 2016, He has been working in the Department of Mathematical Sciences at the Norwegian University of Science and Technology (NTNU) in Trondheim, Norway. He was awarded both the Juan de la Cierva and Ramón y Cajal fellowships. Additionally, he was a fellow of the Studienstiftung des Deutschen Volkes, the Evangelisches Studienwerk e.V., the German Academic Exchange Service (DAAD), and the European Post-Doctoral Institute (EPDI).
NL bialgebras
Speaker: Zohreh Ravanpak (University of Timișoara)
Time: September 26, 2024 15:30-16:30
Venue: 吉林大学数学楼第五研讨室
Abstract: In this talk we introduce the concept of (weak) NL bialgebras. It explores the Poisson-Nijenhuis structures on manifolds within the context of Lie bialgebras. These structures contribute to understanding the interplay between Nijenhuis operators and Lie bialgebras satisfying specific compatibility conditions. They reveal how compatibility conditions facilitate the construction of a hierarchy of compatible Lie bialgebras, both on the original Lie algebra and on its deformed versions through the Nijenhuis structure of any order. We apply our findings to a well-known dynamical system, a particular case of the Euler-top, demonstrating that the underlying algebraic structure of Euler-top dynamics is a weak NL bialgebra. It is based on my recent work: https://arxiv.org/pdf/2404.17708.
Bio: Zohreh Ravanpak completed her PhD in 2018 in Iran, which included a doctoral internship at WSMCS in Warsaw and a six-month research stay at the University of La Laguna (ULL) in Spain. After that, She was a postdoctoral researcher at the Polish Academy of Sciences in Warsaw and the Max-Planck Institute for Mathematics in Bonn. Currently, She is a young researcher at the University of Timișoara în România. Her research focuses on differential geometry and mathematical physics, particularly in the areas of integrable systems (Hamiltonian and bi-Hamiltonian), Poisson geometry, Lie theory, and Lie groupoids.
Symmetric polynomials and identities for n-Lie dialgebras
Speaker: Askar Dzhumadil'daev (Kazakh-British Technical University)
Time: September 21, 2024 14:10-15:10
Venue: 吉林大学正新楼209
Abstract: Polynomial identities for n-Lie dialgebras constructed by symmetric polynomials are studied. Constructions are depend from transposed Poisson structures.
Bio: Askar Dzhumadil'daev is a professor of Kazakh-British Technical University, full member of the Kazakhstan National Academy of Science. His research interests concern cohomologies and deformations of Lie algebras, N-commutators of vector fields, identities of non-associative algebras and operads theory.
Derivations on Operator Algebras and Quantum Dynamics
Speaker: Shavkat Ayupov (V.I.Romanovskiy Institute of Mathematics, Uzbekistan Academy of Sciences)
Time: September 21, 2024 8:30-9:30
Venue: 吉林大学正新楼209
Abstract: This talk presents a full resolution of the problem stated by Ayupov in 2000, and partly restated in 2014 by Kadison and Liu, concerning derivations on algebras of measurable operators affiliated with von Neumann algebras. First we give preliminaries from the theory of operator algebras, non-commutative integration theory and show the physical background of automorphisms and derivations on operator algebras. The second part of the talk explains a background of the Ayupov-Kadison-Liu Problem and its connection with general derivation theory in operator algebras starting with fundamental results due to Kaplanski, Kadison, Sakai and others. We shall cite and briefly explain major results concerning derivations on algebras of unbounded operators and list results concerning some special cases of the problem. Finally, the main result yielding the full resolution will be stated.
Bio: Shavkat Ayupov is the Director of V.I. Romanovskiy Institute of Mathematics, Uzbekistan Academy of Sciences. His field of scientific interest include Theory of Operator Algebras and Quantum Probability, Structure theory of Non-associative algebras (Jordan, Lie, Leibniz, etc.). He is the authors of several monograph devoted to Real and Jordan structures on Operator Algebras, also to the structure theory of Leibniz algebras. Sh. Ayupov is a Member of Uzbekistan Academy of Sciences (since 1995), Fellow of TWAS (The World Academy of Sciences) (since 2003), Senior Associate of ICTP (International Centre for Theoretical Physics) (2008 – 2013), Guest Professor of Sichuan University (Chengdu, China) (2015-2021). He is the Managing Editor of Uzbek Mathematical Journal and editor of “Advances in Operator Theory”. In 2017, he was awarded the State Prize of the first degree in the field of Science and Technology of the Republic of Uzbekistan.
Novel gauge theories and induced mathematical structures
Speaker: Thomas Strobl (University of Lyon)
Venue: 吉林大学数学楼第五研讨室
Abstract: The interaction of mathematics with physics often proved to be very fruitful. In this mini course we focus on the construction of novel type of gauge theories inspired by ideas coming from physics and the mathematical structures that come within this procedure. In this way one is led to novel differential geometric and/or algebraic structures of interest in their own right.
Schedule:

Bio: Thomas Strobl is a professor in the mathematics department at the University of Lyon. His work as a mathematical physicist is mainly concerned with geometric and algebraic aspects of sigma models and gauge theories. In 1993, during his PhD thesis and together with P. Schaller, he discovered the Poisson Sigma Model; it was used later by M. Kontsevich to obtain his famous quantization formula. In 2015 he and A. Kotov introduced a generalisation of Yang-Mills gauge theories to the Lie algebroid setting. In total, in his career he authored more than 60 scientific articles.
Killing metrized exact commutative algebras
Speaker: Daniel Fox (Universidad Politécnica de Madrid)
Time: September 05, 2024 20:00-22:00
Venue: ZOOM ID:904 645 6677, Password:2024
Link: https://zoom.us/j/9046456677?pwd=Y2ZoRUhrdWUvR0w0YmVydGY1TVNwQT09&omn=89697485456
Abstract: A commutative algebra is exact if the traces of its multiplication endormophisms vanish and it is Killing metrized if its Killing-type trace-form is invariant. Such an algebra is neither unital nor associative. Depending on one's background the class of Killing metrized exact commutative algebras may appear either absurdly special or so overbroad as to be hopeless to study. The extensive list of examples includes deunitalizations of étale associative algebras, deunitalizations of semisimple Jordan algebras, tensor products of semisimple Lie algebras, Griess algebras of certain vertex operator algebras, and certain algebras associated with combinatorial structures such as Steiner triple systems. I will motivate studying Killing metrized exact commutative algebras and explain some constructions based on an analogy between curvature of a connection and the associator of an algebra that can be used to organize their study. These will be used to classify algebras over general fields in dimensions at most four and to identify classes of Killing metrized exact commutative algebras susceptible to further study.
Bio: Daniel Fox is a professor of mathematics at the Universidad Politécnica de Madrid in Spain.
Variations on locality
Speaker: Sylvie Paycha (University of Potsdam)
Time: August 24, 2024 11:00-13:00
Venue: 吉林大学数学楼第5研讨室
Abstract: The principle of locality in quantum field theory states that an object is influenced directly only by its immediate surroundings. We introduce locality relations, defined as symmetric binary relations, which capture essential features of locality. Correspondingly we define locality morphisms, namely maps that factorise on products of pairs in the graph of such locality relations. This factorisation is a key property in the context of renormalisation, which served as a motivation for us to introduce the notation of locality in the first place. I will show its efficiency when counting lattice points inside a cone. This apriori infinite cardinal can naturally be renormalised by implementing are gularisation in several variables. There locality plays an essential role in avoiding "fake" finite contributions. It enables a "minimal subtraction scheme" in several variables which singles out a relevant finite part from the a priori infinite cardinal. This is based on joint work with Li Guo and Bin Zhang.
Bio: Sylvie Paycha is a professor at the mathematics department of the University of Potsdam in Germany since 2011 after holding a professorship at the University Clermont-Auvergne in France. She received her PhD at the Ruhr University in Bochum. She works in mathematical physics using tools borrowed from pseudo-differential analysis, geometry and number theory.
Separable Volterra operators and generalized Reynolds algebras
Speaker: Li Guo (Rutgers University-Newark)
Time: August 23, 2024 11:00-13:00
Venue: 吉林大学数学楼第6研讨室
Abstract: The Reynolds operator originated from the well-known work of Reynolds on fluid mechanics in the late 19th century. The classical example of a Reynolds operator is given by a specific Volterra integral operator, first studied by Reynolds and Rota. In this study, we explore the rich algebraic structures from other Volterra integral operators, when the kernel of the operator is separable. The operator satisfies a generalized Reynolds identity, called the D-differential Reynolds identity. To construct the corresponding free objects, we develop a completion for topological operated algebras and define a completion of the shuffle product. The construction provides an algebraic framework to define and study Volterra integral equations with separable kernels. This is a joint work with Richard Gustavson and Yunnan Li.
Bio: 郭锂,美国罗格斯大学纽瓦克分校教授。他的数论工作为怀尔斯证明费马大定理的文章所引用,并将重整化这一物理方法应用于数学研究。他近年来推动Rota-Baxter代数及相关数学和数学物理的研究,应邀为美国数学会在“What Is”栏目中介绍Rota-Baxter代数,并出版这个领域的第一部专著。研究涉及结合代数,李代数,Hopf代数,operad,数论,组合,计算数学,量子场论和可积系统等广泛领域。
S-curvature of homogeneous Finsler spaces
Speaker: Shaoqiang Deng (南开大学数学科学学院)
Time: August 16, 2024 14:00-16:00
Venue: 吉林大学数学楼第5研讨室
Abstract: In this talk, we present our recent results on S-curvature of homogeneous Finsler spaces. We show that a geodesic orbit Finler spaces has vanishing S-curvature. Then we construct some examples of reversible non-Berwald spaces with vanishing S-curvature. We present an explicit formula of the S-curvature of homogeneous Randers spaces, and give a complete classification of homogeneous Randers spaces with positive flag curvature and vanishing S-curvature.
Bio: 邓少强,南开大学数学科学学院教授、博士生导师,享受政府特贴专家。主要从事李群与微分几何的研究,已经在Advances in Mathematics, Crelle's Journal, Transactions AMS等杂志上发表100多篇研究论文,独立撰写的专著《Homogeneous Finsler Spaces》2012年由Springer出版社纽约分社出版,列入著名数学专著系列 Springer Monographs in Mathematics 中。2003年入选教育部优秀青年教师资助计划,2004年入选新世纪优秀人才支持计划,2007年获宝钢全国优秀教师奖,2014年获全国高校自然科学二等奖(第一完成人),2015年获天津市教学名师奖,2016年获天津市五一劳动奖章,2020年被评为天津市劳动模范,2022年获霍英东教育教学二等奖。主持8项国家自然科学基金项目,其中重点项目一项。他是2013-2017和2018-2022年度教育部数学专业教学指导委员会委员。
A bialgebra theory for transposed Poisson algebras via anti-pre-Lie bialgebras
and anti-pre-Lie-Poisson bialgebras
Speaker: Chengming Bai (南开大学陈省身数学研究所)
Time: August 13, 2024 15:00-16:00
Venue: 吉林大学数学楼第5研讨室
Abstract: The approach for Poisson bialgebras characterized by Manin triples with respect to the invariant bilinear forms on both the commutative associative algebras and the Lie algebras is not available for giving a bialgebra theory for transposed Poisson algebras. Alternatively, we consider Manin triples with respect to the commutative 2-cocycles on the Lie algebras instead. Explicitly, we first introduce the notion of anti-pre-Lie bialgebras as the equivalent structure of Manin triples of Lie algebras with respect to the commutative 2-cocycles. Then we introduce the notion of anti-pre-Lie Poisson bialgebras, characterized by Manin triples of transposed Poisson algebras with respect to the bilinear forms which are invariant on the commutative associative algebras and commutative 2-cocycles on the Lie algebras, giving a bialgebra theory for transposed Poisson algebras. This is a joint work with Guilai Liu.
Bio: 白承铭,南开大学陈省身数学研究所教授,所长,南开大学副校长,国务院学位委员会第八届学科评议组成员,教育部核心数学与组合数学重点实验室主任,物理中的群论方法国际大会常务委员会委员。主要从事与数学物理和李理论相关的一些代数体系的结构及其应用的研究。曾获国家杰出青年基金资助和国务院政府特殊津贴,并入选国家“万人计划”科技创新领军人才。培养博士生和硕士生多名,其中的倪翔曾获中国数学会“钟家庆数学奖优秀硕士论文奖”。
Symplectic Morse Theory and Witten Deformation
Speaker: Xiang Tang (美国圣路易斯华盛顿大学)
Time: August 08, 2024 9:00-10:00
Venue: ZOOM ID:904 645 6677, Password:2024
Link: https://zoom.us/j/9046456677?pwd=Y2ZoRUhrdWUvR0w0YmVydGY1TVNwQT09&omn=89697485456
Abstract: In this talk, we will introduce a Morse type cohomology for symplectic manifolds using gradient flows and integration of the symplectic form over spaces of gradient flow lines. We will study this symplectic Morse cohomology using the Witten deformation method. In particular, we will explain that the symplectic Morse cohomology is isomorphic to the cohomology of differential forms introduced by Tsai, Tseng, and Yau for symplectic manifolds. This talk is based on joint works with David Clausen and Li-Sheng Tseng.
Bio: 唐翔,美国圣路易斯华盛顿大学数学系教授。北京大学数学学院2000届本科毕业生。2004年在美国加州大学Berkeley分校数学系取得博士学位。2023年当选AMS Fellow。
Quantum symmetric spaces and Sklyanin determinants
Speaker: Naihuan Jing (North Carolina State University)
Time: July 14, 2024 9:30-10:30
Venue: 吉林大学正新楼209
Abstract: We study the invariant theory of quantum symmetric spaces of symplectic and orthogonal types. Explicitly the quantum symmetric spaces are realized as subrings of the quantum coordinate ring $M_q(N)$ where the relations are given by the quantum minors, Sklyanin determinants, and quantum Pfaffians. One of our results points out that the square of root of quantum determinant is essentially the Sklyanin determinant in a special case, answering a question of Noumi. This is joint work with Jian Zhang(张健).
Bio: 景乃桓,耶鲁大学博士,北卡州立大学终身教授。主要从事无限维李代数、量子群、表示论、代数组合和量子计算方面的研究工作。景乃桓教授在对称函数方面的研究成果被国际上命名为“景氏算子”,在国际主要数学刊物上发表近百篇论文,编辑著作5部。
Symplectic and Contact Geometry of Monge– Ampère equation: Introduction and application
Speaker: Vladimir Rubtsov (Université d’Angers, ITTP Moscow and IGAP Trieste)
Time: June 27, 2024 20:00-21:00
Venue: ZOOM ID:904 645 6677, Password:2024
Link: https://zoom.us/j/9046456677?pwd=Y2ZoRUhrdWUvR0w0YmVydGY1TVNwQT09&omn=89697485456
Abstract: I will present an introduction to the geometric approach to Monge–Ampère operators and equations based on contact and symplectic structures of cotangent and the 1st jet bundles of a smooth manifold. This approach was developed by V. Lychagin and goes back to the ideas of E. Cartan and his successor T. Lepage. I shall try to make my talk self-contained. I also plan to discuss various applications and links with important geometric structures.
Bio: Vladimir Rubtsov graduated in Mathematics from the Moscow State University in 1974 with a MSc in Differential Geometry and Applications. He has a PhD in Higher Geometry and Topology (1983) and held research and teaching positions at various Mathematics and Applied Mathematics Laboratories in the former Soviet Union. Presently he is Professor at the Department of Mathematics, Université d'Angers, and a member of LAREMA (Anjou Research Mathematical Laboratory) of CNRS (France). His research is in the area of Poisson geometry, quantum Groups, integrable systems, symplectic and contact geometric methods in non-linear differential equations and applications in hydrodynamics.
Integrable Peakon Models and Beyond
Speaker: Zhijun Qiao (University of Texas Rio Grande Valley)
Time: June 22, 2024 16:00-17:00
Venue: ZOOM ID:904 645 6677, Password:2024
Link: https://zoom.us/j/9046456677?pwd=Y2ZoRUhrdWUvR0w0YmVydGY1TVNwQT09&omn=89697485456
Abstract: In this talk, we will introduce integrable peakon models developed in recent years and present a basic approach how to get the peakon solutions of integrable equations. In particular, the CH peakon equation is extended to the b-family quadratic and cubic peakon models (FORQ, MOCH, Novikov Equations etc) with peakon and weak-kink solutions. We will also talk about a new CH-type equation – fifth-order CH equation and present new type solutions – pseudo-peakon solutions and their interactions. Some work in the talk is joint with Dr. BQ Xia and Dr. E Reyes. Open problems are proposed in the end for discussion.
Bio: 乔志军教授于1997年获得复旦大学数学系博士学位,从师谷超豪院士和胡和生院士。1997 -1999在北京大学数学学院做博士后。 1999年获得百篇优秀博士毕业论文。1999-2001,德国洪堡基金获得者。现任美国德克萨斯大学数学学院讲席教授,研究方向是非线性偏微分方程,可积系统与非线性尖孤波,KdV方程和孤立子理论,可积辛映射,R-矩阵理论,雷达图像处理和数学物理的反问题。现已出版著作2部,发表论文180余篇,其中包括著名国际杂志《数学物理学通讯》、《非线性科学》等。现作为项目负责人已经完成20多个国家和国际科研项目。组织超过20个国际会议、研讨会。担任国际权威期刊《Studies in Applied Mathematics》编委,以及《Journal of Nonlinear Mathematical Physics》主编。
一类形变李代数的结构与表示
Speaker: 郜云 (加拿大约克大学)
Time: June 18, 2024 15:30-16:30
Venue: 吉林大学正新楼209
Abstract: 扭Heisenberg-Virasoro代数是一类重要的无限维李代数,它与一类曲线的模空间有关。我们对这一李代数的结构与表示进行了系统的研究。
Bio: 郜云,加拿大约克大学教授,德国洪堡学者。主要研究兴趣是高维仿射李代数及相关代数的结构与表示理论。
Hopf trusses an related structures in a monoidal setting
Speaker: Ramón González Rodríguez (University of Vigo)
Time: May 09, 2024 20:00-21:00
Venue: ZOOM ID:904 645 6677, Password:2024
Link: https://zoom.us/j/9046456677?pwd=Y2ZoRUhrdWUvR0w0YmVydGY1TVNwQT09&omn=89697485456
Abstract: The main topic of this talk are certain algebraic structures that in recent years have received attention from numerous mathematicians. More concretely, in this talk we will present, in a braided monoidal setting, the main properties and categorical relationships between the categories of Hopf trusses, weak twisted post-Hopf algebras and weak twisted relative Rota-Baxter operators. The latter objects are a generalisation of the relative Rota-Baxter operators where the Rota-Baxter condition is modified through a cocycle. Also we will present the notion of generalized invertible 1-cocycle and we prove that the category of Hopf trusses is equivalent to the category of generalized invertible 1-cocycles. On the other hand, we also introduce the notions of module for a Hopf truss and for a generalized invertible 1-cocycle. We prove some functorial results involving these categories of modules and we show that the category of modules associated to a generalized invertible 1-cocycle is equivalent to a category of modules associated to a suitable Hopf truss. Finally, assuming the existence of equalizers, we introduce the notion of Hopf-module in the Hopf truss setting and we obtain the Fundamental Theorem of Hopf modules associated to a Hopf truss.
Bio: Ramón González Rodríguez is a full professor at the Departament of Applied Mathematics II in the University of Vigo. His research interests is centered on Hopf algebras and and their generalizations as, for example, weak Hopf algebras, Hopf quasigroupos, groupoids, quasigroupoids, Hopf braces and Hopf trusses. His home page is https://dma.uvigo.es/~rgon/
Mathematics of Imaging Modalities Using Resonant Contrast Agents
Speaker: Mourad Sini (Austrian Academy of Sciences)
Time: May 08-17, 2024
Venue: 正新楼106教室
Introduction: In these lecture, we describe mathematical modeling and analysis of imaging modalities using resonant contrast agents that were recently proposed and highly investigated in the applied engineering community. We offer an original approach to state and solve a family of inverse problems that originate from such imaging modalities.
We start by motivating the need of using contrast agents in imaging (but also in the drugs delivery and therapy modalities at large) and highlight why their resonant effect is the key feature. We describe the close link between the contrast properties of these agents and the classes of resonant frequencies they can generate. These resonant frequencies are characterized as scattering resonances (i.e. generalized eigenvalues) of the related operators. In addition, they are the only frequencies for which the resolvent of this operator is not trivial (does not coincide with the one of the background one, called the free operator). For those resonant frequencies, this resolvent is nothing but the one of the point-supported singular perturbations of the free operator. This point-like perturbation is given as point-source to which is attached a scattering coefficient modeling the interaction between the contrast agent and the surrounding background. In addition, this scattering coefficient reaches its maximum, as a function of the frequency, at the (dominant real part) of the resonant frequencies.
As a consequence of this second characterization, these resonant contrast agents considerably amplify any incident wave (or source) sent at frequencies close to their resonances. This allows to perform quantitative estimates of the background medium using remote measurements. Following this approach, we describe recent results obtained in the frameworks of Ultrasound, Optic and Photo-Acoustic imaging.
Two scenarios are discussed here. In the first one, we use isolated (or closely-spaced) contrast agents. Two general ideas can be highlighted in this case depending whether we use time-harmonic or time- domain measurements:
1. Time-harmonic case. Looking at the measured fields in terms of the incident frequencies, we can recover the related resonances (as the Minnaert or the plasmonic resonances). These resonances have signatures of the background surrounding the location of the used contrast agent.
2. Time-domain case. Looking at the measured fields in terms of time, we can recover the internal values of the travel-time function. This travel-time function provides us the values of the speed of propagation by solving the Eikonal equation.
In the second scenario, these agents are used all-at-once, as a cluster. In this case, we show that we can linearize the boundary maps, as the Neumann-Dirichlet maps, using incident frequencies close to the related resonances. In addition, we derive explicit reconstruction formulas of the medium which enjoy improved stability estimates for the detection. Therefore, using resonant perturbations, we get rid of the nonlinear character and the instability issue of the detection using remote measurements which are the two most inherent drawbacks in using traditional (i.e. contrast agents free) repeated remote measurements.
Finally, as the proposed approach is flexible enough, we describe a larger family of imaging modalities that can fit into the framework and show to what extent we can solve the related inverse problems.
Schedule:
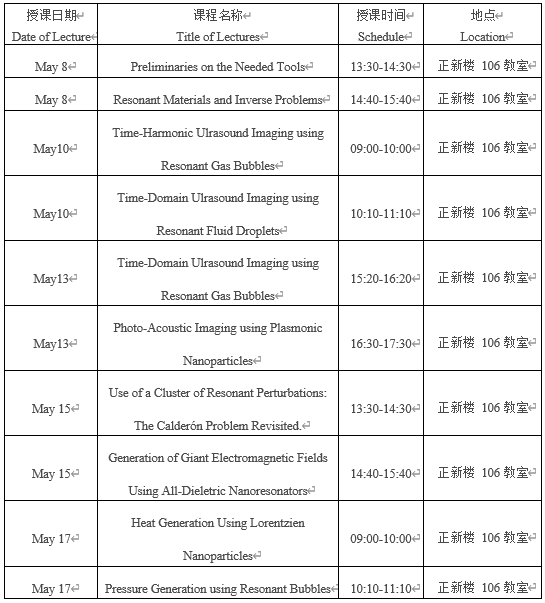
Bio: M. Sini got his PhD degree from University of Provence, France, in October 2002. From September 2006, he joined the Radon Institute, of the Austrian Academy of Sciences, where he was tenured since 2011 as a senior fellow (equivalent to university professor) after securing the Habilitation degree from J. Kepler University in 2009. M. Sini was invited to deliver the IAAM Award Lecture (Sweden, August 2019) and an invited plenary speaker in the Applied Inverse Problems (AIP) conference (Grenoble, France, July 2019). He attracted around 2 Mi euro as third-party funding. M. Sini is interested in the analysis of partial differential equations applied to inverse problems, mathematical imaging, mathematical therapy and material theory. By now, he published nearly 100 papers, most of them in top journals, several book chapters and co-edited a book. He is member of the editorial board of several journals including Mathematical Methods in Applied Sciences (Wiley) and Communication on Analysis and Computation (AIMS).
L-Algebras: The Yang-Baxter equation in algebraic logic
Speaker: Leandro Vendramin (Vrije Universiteit Brussel,Belgium)
Time: April 23, 2024 20:00-22:00
Venue: ZOOM ID:904 645 6677, Password:2024
Link: https://zoom.us/j/9046456677?pwd=Y2ZoRUhrdWUvR0w0YmVydGY1TVNwQT09&omn=89697485456
Abstract: We will discuss interactions between set-theoretical solutions to the Yang-Baxter equation and structures that appear in algebraic logic. Most of this interplay will be based on the recently introduced theory of L-algebras. Hilbert and Heyting algebras are examples of L-algebras. The talk requires almost no background. We will present examples, problems and conjectures.
Bio: Leandro Vendramin is an Associate Professor of Mathematics at the Vrije Universiteit Brussel, Belgium. His research interests are related to the algebra behind the Yang-Baxter equation. This includes Hopf algebras and Nichols algebras and discrete structures such as skew braces and L-algebras. His home page is https://leandrovendramin.org.
A gentle introduction to the Drinfel'd associator
Speaker: Martin Bordemann (Université de Haute Alsace, Mulhouse, France)
Time: April 11, 2024 20:00-21:00
Venue: ZOOM ID:904 645 6677, Password:2024
Link: https://zoom.us/j/9046456677?pwd=Y2ZoRUhrdWUvR0w0YmVydGY1TVNwQT09&omn=87511211646
Abstract: This is a pedagogical talk about the famous associator invented by V.G.Drinfel'd in 1989/90 and a proof of its hexagon and pentagon identities. It is well-known that this associator has applications to the quantization of (quasi) Lie bialgebras (P.I.Etingof-D.A.Kazhdan and B.Enriquez-G.Halbout), deformation quantization (D.E.Tamarkin) and number theory (multiple zeta values) via its rôle in deforming symmetric monoidal categories into braided ones using an `infinitesimal braiding'. Drinfel'd's exposition in the original articles (but also the one in most textbooks) had been quite sketchy, and the mortal reader usually does not know to what extent s/he has to know deep complex analysis, algebraic topology, or conformal field theory. We give a much more elementary and explicit approach using limits of (formal) parallel transports along concrete paths in explicit star-shaped domains of the real line and plane with respect to explicit flat (formal) connections derived from the Knizhnik-Zamolodchikov connection.
Bio: Martin Bordemann is presently a full professor at the mathematics department of the Université de Haute Alsace, Mulhouse, France since 2000. He has done a PhD in mathematical physics on integrable systems with Hartmann Römer in Freiburg, Germany (1990) and a Master of mathematics with Otto Kegel in Freiburg on metrised Lie algebras (1989). His research is centered around deformation quantization, and more general algebraic deformation theory.
A Combinatorial Approach to Homology of Algebraic Systems
Speaker: Viktor Lopatkin (Higher School of Economics)
Time: April 06, 2024 16:00-17:00
Venue: ZOOM ID:904 645 6677, Password:2024
Link: https://zoom.us/j/9046456677?pwd=Y2ZoRUhrdWUvR0w0YmVydGY1TVNwQT09&omn=87511211646
Abstract: It is well known there are many important algebras, groups, semigroups are presented via generators and relations. In other words, we get a set of generators and relations among them. It then arises a question is about relations among relations, relations among relations among relations and so on. It thus gives a “natural” way for appearing of resolutions. This is a homological algebra point of view to study such algebraic structures. In this talk we will get to know about a power and universal method how to construct such resolutions which are call Anick resolutions. This method is based on two big foundations; Groubner--Shirshov bases theory and algebraic discrete Morse theory. We consider how it works in some examples (symmetric group S3) and we also talk about comultiplication of Anick complexes which give arise to multiplication on cohomology.
Bio: Viktor Lopatkin is an associate professor at HSE University (=Higher School of Economics) in Moscow, Russia. He works at Anick resolutions and Groubner-Shirshov bases theory. He also takes an interest at knot theory, vertex algebra theory, Lie algebra theory.
Skew braces and related structures
Speaker: Senne Trappeniers (Vrije Universiteit Brussel)
Time: March 28, 2024 20:00-22:00
Venue: ZOOM ID:904 645 6677, Password:2024
Abstract: Historically, (skew) braces are algebraic structures that arose out of the study of set-theoretic solutions of the Yang-Baxter equation. Braces were defined by Rump in 2006 and skew braces by Guarnieri and Vendramin in 2017. They provide a nice framework to formulate some older results of Etingof, Schedler, Soloviev regarding the Yang-Baxter equation, but also provide new constructions and insights. Since these seminal papers, research around skew braces has both improved the understanding of their interplay with the Yang-Baxter equation, but also unveiled unexpected connections with for example Hopf-Galois extensions, pre-Lie rings and post-Lie algebras. In this talk, the goal is to give an overview of some of these connections and state related open research questions.
Bio: Senne Trappeniers is PhD student at the Vrije Universiteit Brussel under supervision of Leandro Vendramin. His research interests are centered around skew braces, ranging from purely skew brace theoretic questions to connections with other mathematical structures like Hopf-Galois extensions, set-theoretic solutions of the Yang-Baxter equation and pre-Lie rings.
Rota-Baxter operators on groups
Speaker: Aleksei Galt (Sobolev Institute of Mathematics)
Time: March 21, 2024 15:30-16:30
Venue: The fifth seminar room, Mathematics Building
Abstract: Rota-Baxter operators on Lie groups and more generally on groups were introduced by Guo, Lang, and Sheng in 2021. In this talk we discuss some general constructions of Rota-Baxter operators on groups. We describe all Rota-Baxter operators on dihedral and alternating groups.
Bio: Aleksei Galt is a senior researcher of Sobolev Institute of Mathematics and an associate professor of Novosibirsk State University. He finished his PhD thesis “Conjugacy problems in finite groups of Lie type” in 2010. His research interests are finite groups of Lie type, linear algebraic groups, permutation groups and related areas.
Lie brackets on affine spaces
Speaker: Tomasz Brzeziński (Swansea University and University of Białystok)
Time: March 07, 2024 20:00-22:00
Venue: ZOOM ID:904 645 6677, Password:2024
Link: https://zoom.us/j/9046456677?pwd=Y2ZoRUhrdWUvR0w0YmVydGY1TVNwQT09&omn=87511211646
Abstract: We first explore the definition of an affine space which makes no reference to the underlying vector space and then formulate the notion of a Lie bracket and hence a Lie algebra on an affine space in this framework. Since an affine space has neither distinguished elements nor additive structure, the concepts of antisymmetry and Jacobi identity need to be modified. We provide suitable modifications and illustrate them by a number of examples from matrix algebra and geometry.
Bio: Tomasz Brzeziński is a Professor of Mathematics at Swansea University (UK) and University of Białystok (Poland). He is a mathematician specialising in Algebra (in particular studies of various algebraic structures such as rings, modules, corings, comodules, Hopf algebras etc.), Noncommutative Geometry (both algebraic and differential, with particular stress put on symmetry aspects), Category Theory and some aspects of Mathematical Physics (quantum groups, integrable systems). He is the author or co-author of a monograph and over 110 papers (written with ca 45 co-authors). One of his notable achievement is the revival and significant development of the theory of corings (new AMS classification category has been created for corings and comodules as a result of this activity).
Compatible Poisson structures on multiplicative quiver varieties
Speaker: Maxime Fairon (Université de Bourgogne)
Time: February 29, 2024 20:00-22:00
Venue: ZOOM ID:904 645 6677, Password:2024
Link: https://zoom.us/j/9046456677?pwd=Y2ZoRUhrdWUvR0w0YmVydGY1TVNwQT09&omn=87511211646
Abstract: Any multiplicative quiver variety is endowed with a Poisson structure constructed by M. Van den Bergh through reduction from a Hamiltonian quasi-Poisson structure. The smooth locus of this variety carries a corresponding symplectic form defined by D. Yamakama through quasi-Hamiltonian reduction. In this talk, I want to explain how to include this Poisson structure as part of a larger pencil of compatible Poisson structures on the multiplicative quiver variety. The pencil is defined by reduction from a pencil of (non-degenerate) Hamiltonian quasi-Poisson structures, whose construction can be adapted to various frameworks, e.g. in relation to character varieties. I will start by explaining the simpler analogous situation that leads to a pencil of Poisson structures on (additive) quiver varieties, before detailing the multiplicative case. Moreover, I will show that it is possible to understand the construction through the lens of non-commutative Poisson geometry. Time allowing, I may comment on the application of this result to the spin Ruijsenaars-Schneider phase space; this shows the compatibility of two Poisson structures that appeared in independent works of Arutyunov-Olivucci (arXiv:1906.02619) and of Chalykh and myself (arXiv:1811.08727).
Bio: Maxime Fairon is Maître de Conférences (equivalent to lecturer) at Institut de Mathématiques de Bourgogne, Université de Bourgogne, Dijon, France. His research interests are split between: i) classical integrable systems appearing in mathematical physics, and ii) non-commutative Poisson geometry.
Modular classes in Poisson and Jacobi geometry
Speaker: Aissa Wade (Penn State University, USA)
Time: February 22, 2024 21:00-22:00
Venue: ZOOM ID:904 645 6677, Password:2024
Link: https://zoom.us/j/9046456677?pwd=Y2ZoRUhrdWUvR0w0YmVydGY1TVNwQT09&omn=87511211646
Abstract: The modular class of a Poisson manifold is an element of its first Poisson cohomology group, which measures the obstruction to the existence of a measure on this Poisson manifold that is invariant under all Hamiltonian diffeomorphisms The concept of a modular class was extended to general Lie algebroids by Evens, Lu and Weinstein. Recently, there have been various developments and applications of modular classes of Poisson manifolds and Lie algebroids. The main goal of this talk is to introduce modular classes in the more general setting of Jacobi geometry. We will first give a brief review of modular classes in Poisson geometry, and then we will discuss Jacobi manifolds, Jacobi algebroids, and Gerstenhaber Jacobi algebras. Finally, we will introduce modular classes of Jacobi manifolds and Jacobi algebroids.
Bio: Aissa Wade is a professor in the Mathematics Department at Penn State University. She was the Head of the African Institute for Mathematical Sciences (AIMS) center in Senegal from 2016 to 2018. Her research interests lie in Poisson geometry, contact geometry and mathematical physics.
Free post-groups, post-groups from group actions and post-Lie algebras
Speaker: Dominique Manchon (Université Clermont-Auvergne)
Time: February 01, 2024 20:00-21:00
Venue: ZOOM ID:904 645 6677, Password:2023
Link: https://us02web.zoom.us/j/9046456677?pwd=UHErd3RJVzFsNzNnczFZYm9uYlV6QT09
Abstract: After providing a short review on the recently introduced notion of post-group by C. Bai, L. Guo, Y. Sheng and R. Tang, we will exhibit post-group and weak post-group counterparts of important post-Lie algebras in the literature, including the infinite-dimensional post-Lie algebra of Lie group integrators. The notion of free post-group will be examined, and a group isomorphism between the two group structures associated to a free post-group, reminiscent to A. Gavrilov's K-map in differential geometry, will be described. This is a joint work with Mahdi Jasim Hasan Al-Kaabi (Mustansiriyah University, Baghdad, Iraq) and Kurusch Ebrahimi-Fard (NTNU, Trondheim, Norway).
Bio: Dominique Manchon Chargé de Recherches (senior researcher) at CNRS, Laboratoire de Mathématiques Blaise Pascal, Université Clermont-Auvergne, Clermont-Ferrand, France. His research interests are Lie groups and Lie algebras, Hopf algebras and algebraic combinatorics.
Finite generations of Yoneda algebras for complete intersections
Speaker: Zongzhu Lin (Kansas State University)
Time: January 25, 2024 9:00-11:00
Location: ZOOM ID:904 645 6677, Password:2023
Link: https://us02web.zoom.us/j/9046456677?pwd=UHErd3RJVzFsNzNnczFZYm9uYlV6QT09
Abstract:

Bio: 林宗柱,美国堪萨斯州立大学终身教授,博士生导师,曾任三峡数学研究中心主任,美国科学基金会NSF项目主任和《中国科学:数学》编委。主要从事表示论、代数群以及量子群等方面的研究,论文发表在 Invent. Math., Adv. Math., Trans. Amer. Math. Soc., CMP 和J. Algebra 等重要学术期刊上。
Parametrizations of algebraic structures
Speaker: Loic Foissy (Université du Littoral Côte d’Opale (ULCO), Calais, France)
Time: January 11, 2024 20:00-21:00
Location: ZOOM ID:904 645 6677, Password:2023
Abstract: In the last few years, several generalizations of classical objects (associative, dendriform, pre-Lie, Rota-Baxter algebras and others) appear in the literature. In each case, each product is replaced by a family of products indexed by a set (matching objects) or by a semigroup (family objects), with axioms mimicking the classical one in such a way that, loosely speaking, the underlying combinatorics is conserved.
We shall give a way to include all these generalizations in a same frame. This will make appear algebraic structures on the set used for the parametrization, such as extended (di)-associative semigroups, which are (di)-associative semigroups with extra products.
This is a joint work with Dominique Manchon, Xiao-Song Peng and Yuanyuan Zhang.
Bio: Loic Foissy is a professor at the University of the Littoral Cote d’Opale, France. His research domain is Algebraic Combinatorics. More precisely, He works on combinatorial Hopf algebras, operads and their applications.
Can AI do mathematical research?
Speaker: Nguyen Tien Zung (University of Toulouse, France and Torus AI)
Time: December 7, 2023 20:00-21:00
Location: ZOOM ID:904 645 6677, Password:2023
Abstract: In this talk I would like to discuss the question: Can AI (artificial intelligence) do mathematical research, create new beautiful and useful mathematical theories, solve long-standing math problems, and explain all that in an easy to understand way to humans? What are the steps towards building such an AI? What will be the implications for us mathematicians? I will begin the talk by a brief survey of what can AI do for mathematics right now, with examples in problem solving, dynamical systems, etc.
Bio: Nguyen Tien Zung is a pure mathematician turned AI entrepreneur, professor at the University of Toulouse (on leave), founder of the startup Torus AI.
Rota-Baxter operators and coboundary Lie bialgebra structures on perfect finite-dimensional Lie algebras
Speaker: Maxim Goncharov (Sobolev Institute of Mathematics)
Time: December 1, 2023 13:00-14:00
Location: 313 Zhengxin Building
Abstract: There is a connection between structures of a Lie bialgebra on a given quadratic Lie algebra L and Rota-Baxter operators of a special type on L. Namely, there is a classical result that says that structures of a triangular Lie bialgebra on a quadratic Lie algebra L are in one-to-one correspondence with skew-symmetric Rota-Baxter operators of weight zero on L. Another classical result states the connection between factorizable Lie bialgebra structures and Rota-Baxter operators of weight 1 satisfying some generalized skew-symmetry property. In this talk, we will generalize these results and speak on the connection between coboundary Lie bialgebra structures on a perfect quadratic Lie algebra with solutions of the modified classical Yang-Baxter equation and Rota-Baxter operators of special type. Also, we will describe the classical double of a coboundary Lie bialgebra in terms of Rota-Baxter operators. As an application, we will speak on coboundary Lie bialgebra structures on simple, semisimple, and reductive finite-dimensional Lie algebras.
Bio: Maxim Goncharov, Ph.D., Senior research fellow in Sobolev Institute of Mathematics, Associate Professor at Novosibirsk State University.
Solving some Hamiltonian system via the inverse scattering method
Speaker: Xiaomeng Xu (Peking University)
Time: December 1, 2023 11:00-12:00
Location: 313 Zhengxin Building
Abstract: The inverse scattering method, as well as the r-matrix formulation, was designed to study some nonlinear problem via the associated linear one. This talk studies a question of this type. In particular, it finds some special solutions of the Hamiltonian system arising from the theory of isomonodromy deformation.
Bio: 徐晓濛,北京大学助理教授,2016年获日内瓦大学博士学位,主要研究方向是表示论、辛几何、奇点理论及其在数学物理中的应用。目前在Adv. Math., Comm. Math. Phys., Int. Math. Res. Not. 等数学期刊发表多篇论文。
The descriptions of solvable Lie superalgebras of maximal rank
Speaker: Bakhrom Omirov (National University of Uzbekistan)
Time: November 30, 2023 13:30-14:30
Location: 313 Zhengxin Building
Abstract: This report is devoted to the study of the structures of complex Lie superalgebras of maximum rank. Under certain conditions, we will give estimates for upper bounds on the dimensions of subspaces complementary to nilradicals and show that an arbitrary solvable Lie superalgebra of maximal rank is isomorphic to a maximal solvable extension of a nilradical of maximal rank. Some other additional results related to cohomology groups of solvable Lie algebras of maximum rank will be discussed.
Bio: Bakhrom Omirov is a professor at the National University of Uzbekistan. His research focused on non-associative algebras and superalgebras. In particular, he is one of the authors of the monograph devoted to the structure theory of Leibniz algebras. Bakhrom Omirov is a member of The World Academy of Sciences, which includes 66 countries), as well as Uzbek and American Societies.
He is a winner of several prestigious fellowships (Fulbright, USA; INTAS, Belgium).
Graded geometry and applications in physics
Speaker: Vladimir Salnikov (CNRS / La Rochelle University)
Time: November 30 - December 1, 2023
Location: 313 Zhengxin Building
Schedule:
Abstract: In this minicourse I will give an overview of results on various instances of graded geometry, that we have obtained with several colleagues in the last years. I will start with a comparison of definitions of N- and Z- graded manifolds and introduce a way of constructing a filtration of the sheaf of function on the latter one. Then I will turn to differential graded manifolds (also called Q-manifolds) and present a normal for result for a homological vector field on Z-graded manifold. Related constructions have been applied in theoretical physics, namely for studying symmetries and gauging of sigma models - I will comment on that. And in the end I will present one of my motivations to going through the labor of all these construction: the problem of integration of differential graded Lie algebras and some ongoing projects inspired by it.
Bio: Vladimir Salnikov is a researcher at CNRS (National Centre for Scientific Research), La Rochelle University, France. His scientific interests are graded and generalized geometry, dynamical systems, applications to mechanics and theoretical physics.
Syzygy modules and simplicial resolutions
Speaker: Aliaksandr Hancharuk (University Lyon 1)
Time: November 13-16, 2023 21:00-22:00
Location: Zoom id:904 645 6677 Password:2023
Abstract: Hilbert in 1890s famously proved that a graded finitely generated module over a polynomial ring admits a free resolution of finite length. Since then a lot of progress has been done on the structure and properties of finite free resolutions. We will study those underlying some abstract simplicial complex. Lastly, we relate these finite resolutions to the infinite ones and discuss its applications. Based on "Combinatorial commutative algebra" by Miller and Sturmfels, "Graded Syzygies" by Peeva and some new results by the author.
Four subtitles of the minicourse:
1. Graded free resolutions. Koszul complex. Hilbert Syzygy theorem.
2. Simpicial resolutions, Taylor complex, Scarf complex.
3. Duality for resolutions, Alexander duality.
4. Infinite graded resolutions. Tate resolutions.
Bio: Aliaksandr Hancharuk did his Ph.D. in 2023 with Prof.Strobl in University Lyon 1. His research interests and work is concentrated in the intersection of mathematical physics and homological algebra, namely in the algebraic aspects of gauge theories.
Option Pricing with Transaction Costs: Challenges and Approaches
Speaker: Xiaoping Lu (University of Wollongong)
Time: November 9, 2023 10:00-11:00
Location: 数学楼第二报告厅
Abstract: In modern finance, mathematics assumes a pivotal role, particularly in option pricing. However, the consideration of transaction costs introduces a complexity that the conventional notion of a unique fair price between the option holder and writer, no longer exists. Both parties now seek to recover the costs incurred through trading the underlying stocks as part of their hedging strategy, thereby influencing the prices at which they are willing to transact for options. Mathematically, transaction costs make the pricing problem much more complicated, especially for American options. In this talk, some methods we used to price options in the presence of transaction costs will be presented, providing insights into how transaction costs impact option prices and optimal exercise policies for American options.
Bio: Dr. Xiaoping Lu is an Associate Professor in Applied Mathematics and the Director of the Centre for Financial Mathematics at the School of Mathematics and Applied Statistics, University of Wollongong, Australia. Holding a PhD from the University of Michigan, Ann Arbor, USA, Xiaoping’s research journey is marked by a diverse range of interests, with a recent emphasis on financial mathematics. Her recent works have revolved around the valuation of American options and a spectrum of financial derivatives, including Barrier option, convertible bonds, Foreign Exchange, Interest Rate Derivatives, Timer Options, Parisian Options, Stock Loans, and Weather Derivatives. In addition to her publications in top-ranked international journals, Xiaoping has co-edited a special issue on Financial Mathematics and Quantitative Finance for the ANZIAM Journal. She is also an editor at the International Journal of Mathematics for Industry.
Nilpotent Lie algebras with quadratic pseudo-Hermitian metrics
Speaker: Ignacio Bajo (Universidad de Vigo, Spain)
Time: October 26, 2023 20:00-21:00
Location: Zoom ID:904 645 6677 Password:2023
Abstract: We study nilpotent Lie algebras endowed with a complex structure and a quadratic structure which is pseudo-Hermitian for the given complex structure. We propose several methods to construct such Lie algebras and use a method of double extension by planes to get an inductive description of all of them. Such a method let us give a complete classification of nilpotent quadratic Lie algebras where the metric is Lorentz-Hermitian and to obtain a complete classification of pseudo-Hermitian quadratic Lie algebras up to dimension 8 and their inequivalent pseudo-Hermitian metrics.
Bio: Ignacio Bajo works at the Departament of Applied Mathematics II in the University of Vigo and currently the Chair of the Department. His research interests nowadays are focused on Lie algebras and Lie groups but also on other non-associative algebras related to geometrical problems.
Stochastic anticipating equations
Speaker: Andrey Dorogovtsev (Institute of Mathematics,NAS Ukraine)
Time: October 23 -- November 14, 2023
Location: Zoom ID:871 7544 9382 Password:959182
Abstract: This course is devoted to the stochastic anticipating equations with the extended stochastic integral with respect to the Gaussian processes of a special type. Professor Andrey will give students some time to understand the knowledge and give some small questions about the lectures.
Schedule:
Bio: Andrey Dorogovtsev教授是乌克兰国家科学院通讯院士,乌克兰国家科学院数学所随机过程理论系主任,主要从事概率论及其相关领域研究,是乌克兰概率论研究方向学术领军人物之一。Andrey Dorogovtsev教授是乌克兰与德国、乌克兰与俄罗斯等国家联合项目的乌方负责人。同时,Andrey Dorogovtsev教授是《Theory of Stochastic Processes》、《Ukraine Mathematical Journal》等杂志的编委。
Perturbative expansion of Yang-Baxter operators and Lie algebra cohomology
Speaker: Emanuele Zappala (Idaho State University)
Time: October 19, 2023 20:00-21:00
Location: Zoom ID:904 645 6677 Password:2023
Abstract: Self-distributive objects in symmetric monoidal categories are known to produce Yang-Baxter operators, e.g. quandles and their linearization in modules. An important class of self-distributive objects arises from Lie algebras (binary and $n$-ary as well), giving a way of constructing a Yang-Baxter operator from an initial Lie algebra. This allows us to study the relation between self-distributive cohomology, Lie algebra cohomology, and Yang-Baxter cohomology. We therefore obtain a theory of infinitesimal deformations of Yang-Baxter operators that is tightly connected to the deformation theory of Lie algebras and their associated self-distributive objects. In this talk, I will explore these connections and the results that can be shown in this regard. Moreover, I will consider the problem of obtained higher order deformations of the Yang-Baxter operators in relation to the higher deformations of Lie algebras, therefore producing Yang-Baxter operators that are given by a formal power series (perturbative expansion). I will also present several open questions.
Bio: Emanuele Zappala is an assistant professor in the department of Mathematics and Statistics at Idaho State University. His work mainly concerns quantum algebra (Yang-Baxter operators and their cohomology), geometric topology (cohomological invariants of embedded surfaces), applications of algebra and topology to quantum machine learning, and operator learning (iterative methods in deep learning).
Higher order algebroids and representations up to homotopy
Speaker: Mikołaj Rotkiewicz (University of Warsaw. Institute of Mathematics )
Time: September 27, 2023 20:00-21:00
Location: Zoom ID: 904 645 6677 Password:2023
Abstract: The concept of a higher algebroid, as introduced by M. Jóźwikowski and M. Rotkiewicz, naturally generalizes the notions of an algebroid and a higher tangent bundle. The idea is based on a description of (Lie) algebroids as differential relations of a special kind. My goal is to explain the notion of a higher algebroid in a more standard language, i.e. in terms of some bracket operations and vector bundle morphisms. In order two we end up with representation up to homotopy of (Lie) algebroids.
Bio: Mikołaj Rotkiewicz is an academic teacher and a researcher in the Faculty of Mathematics, Informatics and Mechanics in Warsaw. He obtained PhD in the field of Lie groups and Lie algebras. He was granted a fellowship from the Polish Academy of Sciences. Earlier he was awarded in many mathematical competitions. He is an author of a dozen publications in prestigious journals. His mathematical interest lies in graded geometry, theory of supermanifolds, geometric mechanics and recreational mathematics.
Construction of nilpotent Lie algebras with complex structures
Speaker: Adela Latorre (Polytechnic University of Madrid, Spain)
Time: September 21, 2023 17:00-18:00
Location: Zoom ID: 904 645 6677 Password:2023
Abstract: Complex manifolds can be characterized as pairs (M,J), where M is an even-dimensional differentiable manifold and J is a complex structure on it. Although the explicit construction of these J's is a difficult task, the problem can be slightly simplified when M is a nilmanifold and one restricts to the study of invariant complex structures on M. In this case, the problem of finding the pairs (M,J) is related to the classification of real nilpotent Lie algebras with complex structures. Such classification has been completed in real dimensions 4 and 6. However, the same techniques are difficult to apply when the dimension of the nilpotent Lie algebra is equal to or higher than 8. In this talk, we will present a new approach to the problem that will allow us to find every 8-dimensional real nilpotent Lie algebra having one-dimensional center and admitting complex structures.
Bio: Adela Latorre works at the Department of Applied Mathematics of the Polytechnic University of Madrid (Spain). Her main research area is complex non-Kähler geometry, although she is also interested in topics related to Lie algebras and Lie groups.
Pre-Lie algebra structures and etale affine representations
Speaker: Dietrich Burde (University of Vienna, Austria)
Time: September 14, 2023 20:00-21:00
Location: Zoom ID: 904 645 6677 Password:2023
Abstract: Pre-Lie algebras and Post-Lie algebras arise in many areas of mathematics and physics. They are also related to etale affine representations of Lie algebras and algebraic groups. They also arise in the context of affine geometry on Lie groups, operad theory, deformation theory and Young-Baxter equations. For reductive groups, every etale affine representation is equivalent to a linear representation and we obtain a special case of a prehomogeneous representation. Such representations have been classified by Sato and Kimura in some cases. The induced representation on the Lie algebra level gives rise to a pre-Lie algebra structure on the associated Lie algebra. Pre-Lie algebra structures also correspond to left-invariant affine structures on Lie groups. In this talk we present results on the existence of etale affine representations of reductive groups and Lie algebras and discuss a related conjecture of V. Popov concerning flattenable groups and linearizable subgroups of the affine Cremona group.
Bio: Dietrich Burde is a professor at the Department of Mathematics at the University of Vienna. He obtained his Ph.D. in 1992 at the University of Bonn in Germany. His research interests lie in algebra and geometry, in the area of Lie groups, Lie algebras, algebraic groups and representation theory. He has received research grants from the Austrian Science Foundation on the topic "Affine Geometry on Lie Groups and Lie-algebraic Structures".
Semidirect products in digroups, skew braces, heaps, trusses, and in universal algebra
Speaker: Alberto Facchini (University of Padua)
Time: September 7, 2023 20:00-21:00
Location: Zoom ID: 904 645 6677 Password:2023
Abstract: We will present some algebraic structures that have recently received attention in view of their relation with set theoretic solutions of the Yang-Baxter equation. We will present the basic properties of digroups, skew braces, heaps, and trusses. In particular, we will focus on their semidirect products.
Bio: Alberto Facchini has been full professor of Algebra until 1999 at the University of Udine, and from 1999 to 2022 at the University of Padua. Now he is an Emeritus Professor. He has had six PhD students and has written more than 170 research papers published in mathematical journals, four textbooks, and two research books published by Birkhäuser Verlag (Basel). He is a member of Accademia San Marco and Accademia Galileiana di Scienze Lettere ed Arti in Padova. He has given scientific communications and lectures in almost 40 different countries. He has been one of the editors of a dozen mathematical journals, among which Bollettino dell'Unione Matematica Italiana, Communications in Algebra, Journal of Algebra and Its Applications, Journal of the Egyptian Mathematical Society, and Rendiconti del Seminario Matematico dell'Università di Padova. In Udine he has been dean of the Faculty of Science, in Padua he has been director of the Department of Pure and Applied Mathematics.
Introduction to Noncommutative Isolated Singularities and Resolutions
Speaker: Quanshui Wu (Fudan University)
Time: August 23, 2023 10:30-11:30
Location: 正新楼313室
Abstract: This will be an introductory talk to noncommutative isolated singularities and resolutions. I will recall some examples of commutative isolated singularities and noncommutative isolated singularities first. Then I will survey some related results, and introduce a version of noncommutative resolutions of commonly graded AS-Gorenstein singularities.
Bio: 吴泉水,复旦大学数学科学学院教授、博导、上海数学中心执行主任,主要从事非交换环论、非交换射影代数几何、Hopf代数的同调理论方面的研究。曾获教育部科技进步二等奖、教育部霍英东教育基金会青年教师奖、教育部高校“青年教师奖”、宝钢优秀教师奖、上海市优秀学术带头人、上海市优秀青年教师等,在Duke Math. J.、Trans. Amer. Math. Soc.、Israel J. Math.、J. Noncommut. Geom.、J. Algebra、J. Pure Appl. Algebra等国际著名期刊发表SCI论文50余篇,多次主持国家自然科学基金面上项目,曾担任SCI杂志Comm. Algebra编委。
Noncommutative moduli spaces
Speaker: Andrey Lazarev (Lancaster University)
Time: August 21-25, 2023
Location: 正新楼313室
Abstract: The aim of this minicourse is to outline the construction of global moduli spaces of different objects of algebraic and geometric nature (such as flat connections in vector bundles, modules over associative algebras, objects in dg categories etc.) in a homotopy invariant context. The first part of the course will explain how the local Koszul duality of Hinich and Keller-Lefevre provides a suitable context for studying local moduli problems (also known as deformations). The second part is devoted to the more recent work constructing the corresponding global theory. The global theory shares some properties with the local one but involves several significantly new features, most notably the use of dg categories. The emphasis will be placed on explaining the conceptual picture rather than on technical proofs. Various instructive examples will be given.
Bio: Andrey Lazarev,英国兰卡斯特大学教授,从事代数拓扑与同伦论的研究, Bull. Lond. Math. Soc.杂志主编,在Adv. Math.、 Proc. Lond. Math. Soc.、 J. Noncommut. Geom.等杂志上发表多篇高水平论文。
|
授课日期 Date of Lecture |
课程名称(讲座题目) Name (Title) of Lecture |
授课时间 Duration (Beijing Time) |
参与人数 Number of Participants |
|
Aug 21, 2023 |
Maurer-Cartan (MC) elements and gauge transformations. Deformation theory |
10:30-11:30 |
30 |
|
Aug 21, 2023 |
Model categories and infinity categories, examples: dg algebras and dg Lie algebras |
16:30-17:30 |
30 |
|
Aug 22, 2023 |
Coalgebras and Lie-commutative Koszul duality. |
10:30-11:30 |
30 |
|
Aug 22, 2023 |
Representability of deformation functors |
16:30-17:30 |
30 |
|
Aug 24, 2023 |
MC elements in dg associative algebras and associated dg categories. Homotopy gauge equivalences |
10:30-11:30 |
30 |
|
Aug 24, 2023 |
Homotopy theory of dg categories |
16:30-17:30 |
30 |
|
Aug 25, 2023 |
Global Koszul duality as a Quillen equivalence between infinity-categories of dg algebras and dg coalgebras |
10:30-11:30 |
30 |
|
Aug 25, 2023 |
Representability of noncommutative moduli space functors |
16:30-17:30 |
30 |
On the volume of hyperbolic tetrahedron
Speaker: Nikolay Abrosimov (Sobolev Institute of Mathematics of RAS)
Time: August 20, 2023 10:30-11:30
Location: 正新楼313室
Abstract: The talk will give an overview of the latest results on finding exact formulas for calculating the volumes of hyperbolic tetrahedra. The classical formula of G. Sforza [1] expresses the volume of a hyperbolic tetrahedron of a general form in terms of dihedral angles. Its modern proof is proposed in [2]. The formula in terms of edge lengths is obtained in the recent joint work of the author with B. Vuong [3]. The known formulas for the volume of a hyperbolic tetrahedron of a general form are very complicated and cannot always be applied to calculate the volumes of more complex polyhedra. So, a natural question arises to find more convenient and simple formulas for sufficiently wide families of hyperbolic tetrahedra. At the end of the talk, we will consider hyperbolic tetrahedra of special types: ideal, biorthogonal, 3-orthogonal and their generalizations. The volume of the ideal and biorthogonal tetrahedron was known to N.I. Lobachevsky. We will present new formulas for calculating volumes and normalized volumes of a trirectangular hyperbolic tetrahedron [4] as well as its generalization for the 4-parameter family of tetrahedra with one edge orthogonal to the face. The latter formulas can be used to calculate the volumes of more complex polyhedra in the Lobachevsky space.
References:
[1] G. Sforza, Spazi metrico-proiettivi // Ricerche di Estensionimetria Integrale, Ser. III, VIII (Appendice), 1907, P. 41–66.
[2] N.V. Abrosimov, A.D. Mednykh, Volumes of polytopes in constant curvature spaces // Fields Inst. Commun., 2014, V. 70, P. 1–26. arXiv:1302.4919.
[3] N. Abrosimov, B. Vuong, Explicit volume formula for a hyperbolic tetrahedron in terms of edge lengths // Journal of Knot Theory and Its Ramifications, 2021, V. 30, No. 10, 2140007. arXiv:2107.03004.
[4] N. Abrosimov, S. Stepanishchev, The volume of a trirectangular hyperbolic tetrahedron // Siberian Electronic Mathematical Reports, 2023, V. 20, No. 1, P. 275–284.
Bio: Professor Nikolay Abrosimov is a professor at the Department of Mechanics-Mathmatics of Novosibirsk State University. He received a Candidate of Sciences in physics and mathematics in 2009 from the Sobolev Institute of Mathematics. His research interests are hyperbolic geometry, volumes of non-Euclidean polytopes, geometry and topology of three-dimensional manifolds, orbifolds, knots and links. He has more than 25 research publications. He is a chairman of the Council of Scientific Youth of the Institute of Mathematics of the Siberian Branch of the Russian Academy of Sciences.
Volumes of generalized hyperbolic polyhedra and hyperbolic links
Speaker: Andrei Vesnin (Sobolev Institute of Mathematics of RAS)
Time: August 20, 2023 09:30-10:30
Location: 正新楼313室
Abstract: A polyhedron in a three-dimensional hyperbolic space is said to be generalized if finite, ideal and truncated vertices are admitted. In virtue of Belletti's theorem (2021) the exact upper bound for volumes of generalized hyperbolic polyhedra with the same one-dimensional skeleton G is equal to the volume of an ideal right-angled hyperbolic polyhedron whose one-dimensional skeleton is the medial graph for G. We will present the upper bounds for the volume of an arbitrary generalized hyperbolic polyhedron, where the bonds linearly depend on the number of edges. Moreover, it is shown that the bounds can be improved if the polyhedron has triangular faces and trivalent vertices. As an application there are obtained new upper bounds for the volume of the complement to the hyperbolic link having more than eight twists in a diagram. The results under discussion are based on the preprint arXiv:2307.04543 (https://arxiv.org/abs/2307.04543).
Bio: Professor Andrei Vesnin is head of the Laboratory of Applied Analysis, Sobolev Institute of Mathematics and a professor of Geometry and Topology, Novosibirsk State University. He received a Candidate of Sciences in physics and mathematics in 1991 from the Sobolev Institute of Mathematics for the thesis “Discrete groups of reflections and three-dimensional manifolds”, and a Doctor of Sciences in physics in mathematics in 2005 for the thesis “Volumes and isometries of three-dimensional hyperbolic manifolds and orbifolds”.
Professor Vesnin's research interests include low-dimensional topology, knot theory, hyperbolic geometry, combinatorial group theory, graph theory and applications. In 2008, Prof. Vesnin was elected as corresponding member of the Russian Academy of Sciences. He is a member of the editorial board of the journal "International Journal of Mathematics and Computer Science", and doctoral dissertation council at the Institute of Mathematics SB RAS.
Yang-Baxter equation, Rota-Baxter operators and corresponding algebraic systems
Speaker:Valeriy Bardakov (Tomsk State University)
Time:2023年6月28日 14:30-15:30
Location:吉林大学数学楼3楼第5研讨室
Abstract: Yang-Baxter equation is a famous equation in mathematical physics, knot theory and braid theory. There are different generalization of this equation. In particular, tetrahedron equation and n-simplex equation. To describe solutions of these equations where introduced different algebraic systems: rack, quandle, skew brace and some other. The Yang-Baxter equation connects with Rota-Baxter operator on some algeras and groups. Im this talk we will speak on this things and connections between them.
Bio: Valeriy Bardakov is from Tomsk State University. He is a professor of department of algebra and mathematical logic, Faculty of Mechanic-Mathematics, Tomsk State University. His research interests are group theory, knot theory, braid group, automorphism group, symmetric group, PDE, multidimensional inverse problem, evolution equations and integral geometry. He is an author of more than 100 publications.
Since 1995, he has been running the algebraic seminar, "Evariste Galois", at NSU. Since 2000, together with A. Yu. Vesnin, he has been teaching a special course "Algebraic Methods in Knot Theory" at Novosibirsk State University. In 1993, he won the prize M. I. Kargapolov for young mathematicians for solving problems of the Kourovskaya Notebook.
Simplicial structure on pure singular braid groups of camomile type
Speaker:Tatiana Kozlovskaia (Tomsk State University)
Time:2023年6月28日 13:30-14:30
Location:吉林大学数学楼3楼第5研讨室
Abstract: In my talk we recall some definitions from Knot Theory, Braid Theory and the construction of J. Wu and F. Cohen which connects braid groups and homotopy groups of 2-sphere. In more detail we discuss singular braid groups and its subgroup of pure singular braid group. We describe presentation of these groups and linear representation.
Bio: Tatiana Kozlovskaia is from Scientific and Educational Mathematical Center of Tomsk State University. She is an associated professor of Department of Geometry, Faculty of Mechanic-mathematics, Tomsk State University. Her research interests are 3-dimensional topology, theory of 3-manifolds, low-dimensional geometry, Lens spaces, and Fundamental polyhedra.
Contact geometry via homogeneous symplectic geometry with applications
Speaker:Katarzyna Grabowska (University of Warsaw, Department of Physics)
Time:2023年5月24日 18:00-20:00
Meeting ID:ZOOM Id:904 645 6677,Password:2023
会议链接:
https://us02web.zoom.us/j/9046456677?pwd=UHErd3RJVzFsNzNnczFZYm9uYlV6QT09
Abstract: During the talk she will present the novel approach to contact geometry according to which contact structures are not `odd-dimensional generalizations’ of symplectic geometry but rather particular examples of symplectic geometry, namely homogeneous symplectic principal bundles (with an action of the multiplicative group of non-zero reals). In this setting we are able to construct contact Hamiltonian vector fields even if the global contact form does not exist on the contact manifold in question. The homogeneous symplectic language is also suitable for contact Hamilton-Jacobi theory and contact reductions.
Bio: Katarzyna Grabowska works in the Department of Mathematical Methods in Physics at the Faculty of Physics. She is interested in differential geometric methods in physics and differential geometry in general.
Topological K-theory of discrete groups
Speaker:Bailing Wang (The Australian National University)
Time:2023年5月19日 10:30-11:30
Meeting ID:腾讯会议:516-539-518
Abstract: In the 1980’s motivate by the Atiyah-Singer index formula, Baum and Connes constructed a topological K-theory of a discrete group $\Gamma$, together with an assembly map $\mu$ from this mysterious group to the K-theory group of the reduced C^∗ -algebra of $\Gamma$. They conjectured that this assembly map is an isomorphism. The validity of this conjecture implies Novikov conjecture, Gromov-Lawson-Rosenberg conjecture and Kadison-Kaplansky conjecture.
The mathematical details of this construction and the well-definedness of the assembly map were somewhat missing in their original paper. I will briefly explain some of my earlier work with Paulo Carrillo Rouse on filling up these details, and some recent work with Paulo Carrillo Rouse and Hang Wang on an assembly map to periodic cyclic homology and the Chern-Connes pairing formula for any discrete group.
Bio: 王百灵,澳大利亚国立大学教授。1998 年 4月毕业于澳大利亚阿德莱德大学并获得博士学位。毕业先后在德国波恩马普所,法国高等科学研究所, 苏黎士大学做博士后和访问学者。2005年至今在澳大利亚国立大学工作。主要研究规范场理论在低维拓扑中的拓扑不变量、twisted K-同调和twisted指标理论、Gromov-Witten模空间和哈密尔顿Gromov-Witten模空间的K-理论等领域。
LIE GROUPOIDS IN INFORMATION GEOMETRY
Speaker:Janusz Grabowski (Polish Academy of Sciences)
Time:2023年5月10日 15:50-16: 50
Meeting ID:ZOOM Id:904 645 6677,Password:2023
会议链接:
https://us02web.zoom.us/j/9046456677?pwd=UHErd3RJVzFsNzNnczFZYm9uYlV6QT09
Abstract: After a general introduction to the information geometry, I will show that a natural general setting for statistical and information geometry is the one provided by Lie groupoids and Lie algebroids. The contrast functions are defined on Lie groupoids and give rise to a two-form and a three-form on the corresponding Lie algebroid. If the two-form is non-degenerate, it defines a pseudo-Riemannian metric on the Lie algebroid and a family of Lie algebroid torsion-free connections, including the Levi-Civita connection of the metric. In this framework, the standard two-point contrast functions are understood as functions on the pair groupoid MxM and generate a standard (pseudo-)Riemannian metrics on M, and families of affine connections on the Lie algebroid TM.
Bio: Professor Janusz Grabowski is the Head of the Department of Mathematical Physics and Differential Geometry in the Institute of Mathematics, Polish Academy of Sciences. His main interests are differential geometry and mathematical physics. As an author of about 140 scientific papers, he published fundamental results on Lie algebras of vector fields, diffeomorhism groups, Lie systems, Poisson and Jacobi manifolds, Lie groupoids and algebroids, Lagrangian and Hamiltonian mechanics (including mechanics on contact manifolds), supergeometry, geometry of quantum states and entanglement, etc. His personal page is https://www.impan.pl/~jagrab/.
Regular subgroups, skew braces, gamma functions and Rota–Baxter operators
Speaker:Andrea Caranti (University of Trento, Italy)
Time:2023年4月19日 20:00-22:00
Meeting ID:ZOOM Id:904 645 6677,Password:2023
会议链接:
https://us02web.zoom.us/j/9046456677?pwd=UHErd3RJVzFsNzNnczFZYm9uYlV6QT09
Abstract: Skew braces, a novel algebraic structure introduced only in 2015, have already spawned a sizeable literature. The skew braces with a given additive group structure correspond to the regular subgroups of the permutational holomorph of such a group. These regular subgroups can in turn be described in terms of certain so-called gamma functions from the group to its automorphism group, which are characterised by a functional equation. We will show how gamma functions can be used in studying skew braces, underlining in particular their relationship to Rota-Baxter operators.
Bio: Andrea Caranti is a Senior Professor of Algebra at the University of Trento, Italy. He has worked mainly in group theory (nilpotent groups, automorphisms, applications to cryptography) and on graded, modular Lie algebras. His recent work concerns group-theoretical aspects of skew braces.
On pseudo-Euclidean Lie algebras whose Levi-Civita product is left Leibniz
Speaker:Said Benayadi (University of Lorraine-Metz)
Time:2023年3月30日 20:00-21:00
Meeting ID:ZOOM Id:904 645 6677,Password:2023
会议链接:
https://us02web.zoom.us/j/9046456677?pwd=UHErd3RJVzFsNzNnczFZYm9uYlV6QT09
Abstract: We study a class of Lie algebras which contains the class of quadratic Lie algebras and the class of Milnor Lie algebras, namely, Lie algebras endowed a pseudo-Euclidean metric such its Levi- Civita product is left Leibniz. We call them Levi-Civita left Leibniz Lie algebras LCLL for short. We show that a Lie group (G, h) endowed with a left invariant pseudo-Riemannian such that the corresponding Lie algebra is LCLL is complete and locally symmetric. Moreover, we prove that any Euclidean LCLL Lie algebra is the product of quadratic a Lie algebra and a flat Euclidean Lie algebra. We develop an adapted version of the process of double extension to construct LCLL Lie algebras. We show that Lorentzian or flat LCLL Lie algebras can be obtained by this process.
Bio: Said Benayadi is a professor in University of Lorraine-Metz. His research interest is nonassociative algebras.
Singular foliations and Q-manifolds
Speaker:Camille Laurent-Gengoux (Université de Lorraine, Metz)
Time:2023年3月22日 16:00-17: 00
Meeting ID:ZOOM ID:904 645 6677,Password:2023
会议链接:
https://us02web.zoom.us/j/9046456677?pwd=UHErd3RJVzFsNzNnczFZYm9uYlV6QT09
Abstract: In this talk, we will explain how a Q-manifold (equivalently, a Lie infinity algebroid) can be associated to a singular foliation, and how this Q-manifold helps in studing the geometry of the latter. Joint works with Sylvain Lavau, Ruben Louis, Leonid Ryvkin, Thomas Strobl.
Bio: Camille Laurent-Gengoux is a professor in Université de Lorraine, Metz. He mainly studies Poisson geometry and related structures. He authored more than 40 scientific articles in J. Eur. Math. Soc., Math. Ann., Adv. Math., Int. Math. Res. Not. and other journals.
On a certain family of vertex algebras associated with vertex algebroids
Speaker:Haisheng Li (Rutgers University-Camden)
Time:2023年3月9日 09:00-10:00
Meeting ID:ZOOM Id:904 645 6677,Password:2023
会议链接:
https://us02web.zoom.us/j/9046456677?pwd=UHErd3RJVzFsNzNnczFZYm9uYlV6QT09
Abstract: This talk is about a family of vertex algebras associated with vertex algebroids, constructed by Gorbounov, Malikov, and Schechtman. As the main result, we classify all the (graded) simple modules for such vertex algebras and we show that the equivalence classes of graded simple modules one-to-one correspond to the equivalence classes of simple modules for the Lie algebroids associated with the vertex algebroids. To achieve our goal, we construct and exploit a Lie algebra from a given vertex algebroid. This talk is based on a joint work with Gaywalee Yamskulna.
Bio: Haisheng Li is a professor of Rutgers University-Camden. His main research is on vertex operator algebras and quantum vertex algebras. Among the main results are conceptual constructions of vertex algebras and their modules, twisted modules; A theory of quasi modules; A theory of (weak) quantum vertex algebras and φ-coordinated modules; A conceptual association of double Yangians and quantum affine algebras with quantum vertex algebras. He published more than 100 articles in Duke Math. J., Com. Math. Phys., Adv. Math., Tans. AMS and other Internationally renowned journals.
On local integration of Lie brackets
Speaker:María Amelia Salazar Pinzón (Universidade Federal Fluminense)
Time:2023年2月16日 21:00-22:00
Meeting ID:ZOOM Id:904 645 6677,Password:2023
会议链接:
https://us02web.zoom.us/j/9046456677?pwd=UHErd3RJVzFsNzNnczFZYm9uYlV6QT09
Abstract: The foundation of Lie theory is Lie's three theorems that provide a construction of the Lie algebra associated to any Lie group; the converses of Lie's theorems provide an integration, i.e. a mechanism for constructing a Lie group out of a Lie algebra. The Lie theory for groupoids and algebroids has many analogous results to those for Lie groups and Lie algebras,however, it differs in important respects: one of these aspects is that there are Lie algebroids which do not admit any integration by a Lie groupoid. In joint work with Cabrera and Marcut, we showed that the non-integrability issue can be overcome by considering local Lie groupoids instead. In this talk I will explain a construction of a local Lie groupoid integrating a given Lie algebroid and I will point out the similarities with the classical theory for Lie groups and Lie algebras.
Bio: María Amelia is a professor at Departamento de Matemática Aplicada (GMA) of the Universidade Federal Fluminense (UFF), Brazil.The main research interests are Lie groupoids, Lie algebroids, Lie pseudogroups, geometry of PDE's, Poisson geometry, contact and symplectic geometry.
Local and 2-local derivations and automorphisms of Octonian algebras
Speaker:Shavkat Ayupov (Institute of Mathematics, Uzbekistan Academy of Sciences)
Time:2023年2月9日 16:00-17:00
Meeting ID:ZOOM Id:904 645 6677,Password:2023
会议链接:
https://us02web.zoom.us/j/9046456677?pwd=UHErd3RJVzFsNzNnczFZYm9uYlV6QT09
Abstract:
The talk is devoted to description of local and 2-local derivations (respectively, automorphisms) on octonian algebras. We shall give a general form of local derivations on the octonion algebra O(F) over a field F with zero characteristic. This description implies that the space of all local derivations on O(F) when equipped with Lie bracket is isomorphic to the Lie algebra so7 O(F) of all real skew-symmetric 7 × 7-matrices over F. At the same time the Lie algebra of all derivations are isomorphic to the exceptional Lie algebra g2(F). It follows that the octonion algebra O(F) and Malcev algebra M7(F) over the field F are simple non associative algebras which admit pure local derivations, that is, local derivations which are not derivation.
Further we consider 2-local derivations on the octonion algebra O(F) over an algebraically closed field F and prove that every 2-local derivation on O(F) is a derivation. But for the field R of real numbers 2-local derivations on the octonian algebra O(R) form a Lie algebra which is essentially larger than the Lie algebra g2(R) of derivations. we apply these results to problems for the simple 7-dimensional Malcev algebra. We shall give a general form of local automorphisms on the octonion algebra O(F). This description implies that the group of all local automorphisms on O(F) is isomorphic to the group O7(F) of all orthogonal 7 × 7-matrices over F, and it is essentially larger than the group of all automorphisms.
We also consider 2-local automorphisms on the octonion algebra O(F) over an algebraically closed field F and prove that every 2-local automorphism on O(F) is an automorphism. At the same time the group of 2-local automorphisms of O(R) is larger than the group of automorphisms of O(R). As a corollary we obtain descriptions of local and 2-local automorphisms of seven dimensional simple Malcev algebra.
Bio: Shavkat Ayupov is the Director of V.I. Romanovskiy Institute of Mathematics, Uzbekistan Academy of Sciences. His field of scientific interest include Theory of Operator Algebras and Quantum Probability, Structure theory of Non-associative algebras (Jordan, Lie, Leibniz, etc.). He is the authors of several monograph devoted to Real and Jordan structures on Operator Algebras, also to the structure theory of Leibniz algebras. Sh. Ayupov is a Member of Uzbekistan Academy of Sciences (since 1995), Fellow of TWAS (The World Academy of Sciences) (since 2003), Senior Associate of ICTP (International Centre for Theoretical Physics) (2008 – 2013), Guest Professor of Sichuan University (Chengdu, China) (2015-2021). He is the Managing Editor of Uzbek Mathematical Journal and editor of “Advances in Operator Theory”.
In 2017, he was awarded the State Prize of the first degree in the field of Science and Technology of the Republic of Uzbekistan.
Arborescent Koszul-Tate resolutions and BFV for singular coisotropic reductions
Speaker:Thomas Strobl (University of Lyon)
Time:2023年1月12日 20:00-21:00
Meeting ID:ZOOM Id:904 645 6677,Password:2023
会议链接:
https://us02web.zoom.us/j/9046456677?pwd=UHErd3RJVzFsNzNnczFZYm9uYlV6QT09
Abstract:
Bio:Thomas Strobl is a professor in the mathematics department at the University of Lyon. His work as a mathematical physicist is mainly concerned with geometric and algebraic aspects of sigma models and gauge theories. In 1993, during his PhD thesis and together with P. Schaller, he discovered the Poisson Sigma Model; it was used later by M. Kontsevich to obtain his famous quantization formula. In 2015 he and A. Kotov introduced a generalisation of Yang-Mills gauge theories to the Lie algebroid setting. In total, in his career he authored more than 60 scientific articles.
Subalgebras of free algebras
Speaker:Vladimir Dotsenko (University of Strasbourg)
Time:2023年1月5日 16:00-17:00
Meeting ID:ZOOM Id:904 645 6677,Password:2023
会议链接:
https://us02web.zoom.us/j/9046456677?pwd=UHErd3RJVzFsNzNnczFZYm9uYlV6QT09
Abstract:A classical result going back to works of Shirshov and Witt in 1950s states that every subalgebra of the free Lie algebra is free. Understanding what makes a variety of algebras satisfy this property has been an important open question in ring theory, recorded, for instance, in the Dniester Notebook. I shall talk about a recent work with Ualbai Umirbaev in which we developed a method that allowed us to exhibit infinitely many varieties of algebras (with one binary operation) satisfying this property; prior to our work, only six such varieties had been known. One surprising consequence of our work is that for the variety of all right-symmetric algebras subalgebras of free algebras are free.
Bio:Vladimir Dotsenko is a professor at the University of Strasbourg, France. His work applies ideas of category theory to concrete questions of algebra, combinatorics, geometry and topology.
On the subspaces and quotients of C(K) spaces with few operators
Speaker:ALIRIO GOMEZ GOMEZ (Institute of Science and Technology of the Federal University of São Paulo) (ICT-UNIFESP)
Time:2022年12月15日 20:00-21:00
Meeting ID:Zoom ID:862 062 0549,Password:2022
会议链接:
https://us02web.zoom.us/j/8620620549?pwd=bGhsaG15WjRza2V3ZEN4TzJYZ1FZQT09
Abstract:

Bio:At this moment he is a postdoc student at Federal University of São Paulo, where he is studying Lipschitz free Banach spaces and their applications. Also, he has continued working on Banach spaces C(K) with few operators which was the topic of his doctoral dissertation. As a result, a manuscript on the subspaces of linear operators on C(K) contained in the set of not weak multiplier operators is being completed in collaboration with R. Fajardo and L. Pellegrini. Before he joints UNIFESP, he pursued his PhD in mathematics. In his PhD thesis they found some topological conditions on a compact K, related to the property of C(K) having few operators. They also proved that there exists an indecomposable C(K) that has some not weak multiplier operators. Moreover, assuming the Diamond Principle, they constructed a compact non-weakly Koszmider Space K, which has no trivial retractions. In the next couple of months he will move to Rio de Janeiro where he will be a Professor at Rio de Janeiro State University.
Stokes phenomenon and representation of quantum groups
Speaker:Xiaomeng Xu (Peking University)
Time:2022年12月8日 15:30-16:30
Meeting ID:
Zoom ID:862 062 0549,Password:2022
会议链接:
https://us02web.zoom.us/j/8620620549?pwd=bGhsaG15WjRza2V3ZEN4TzJYZ1FZQT09
Abstract:Stokes phenomenon states that the asymptotic behavior of functions can differ in different regions of the complex plane, and that these differences can be described in a quantitative way. The quantities, the so-called Stokes matrices, have played important roles in many subjects. This talk gives an introduction to the Stokes phenomeon of a meromorphic linear system of ordinary differential equations,and then discusses various unsolved analysis problems, with a relation to the representation theory of quantum groups.
Bio:徐晓濛,北京大学助理教授,2016年获日内瓦大学博士学位,主要研究方向是表示论、辛几何、奇点理论及其在数学物理中的应用。目前在Adv. Math., Comm. Math. Phys., Int. Math. Res. Not. 等数学期刊发表多篇论文。
Some constructions from graded geometry
Speaker:Vladimir Salnikov (CNRS / La Rochelle University)
Time:2022年12月1日 15:30-16:30
Meeting ID:Zoom ID:862 062 0549,Password:2022
https://us02web.zoom.us/j/8620620549?pwd=bGhsaG15WjRza2V3ZEN4TzJYZ1FZQT09
Abstract:In this talk I introduce some natural constructions from the "graded world", paying particular attention to the differences between N- and Z- graded manifolds. I will start by the construction of the sheaf of functions on graded manifolds and describe its structure. The intrinsic properties of this functional space are conveniently given using the language of filtrations, allowing to formulate the analog of Batchelor’s theorem. Afterwards I will briefly introduce graded Hopf algebras and Harish-Chandra pairs, which in turn provide the result of equivalence of categories between graded Lie groups and algebras. These constructions are then used to solve the integration problem of differential graded Lie algebras to differential graded Lie groups. Time permitting, I will also say a few words on canonical forms of differential graded manifolds.
Bio:Vladimir Salnikov is a researcher at CNRS (National Centre for Scientific Research), La Rochelle University, France. His scientific interests are graded and generalized geometry, dynamical systems, applications to mechanics and theoretical physics.
Racks, Leibniz algebras and rack bialgebras
Speaker:Friedrich Wagemann (University of Nantes)
Time:2022年11月29日-12月2日
Meeting ID:Zoom ID:862 062 0549,Password:2022
Abstract:Groups, Lie algebras and associative bialgebras are linked by various functors which are important in Lie theory. We argue that this triad may be generalized to Racks, Leibniz algebras, rack bialgebras, which enjoy roughly the same links. In this minicourse, we will mainly discuss the cohomology of these structures.
|
Date of Lecture |
Name (Title) of Lecture |
Beijing Time |
|
November29, 2022 |
Groups,Lie algebras and associative bialgebras |
20:00-21:00 |
|
November29, 2022 |
Racks, Leibniz algebras and rack bialgebras |
21:00-22:00 |
|
November30, 2022 |
Cohomology of Racks |
20:00-21:00 |
|
November30, 2022 |
Periodicity in algebraic K-theory |
21:00-22:00 |
|
December1, 2022 |
Cohomology of Leibniz algebras |
20:00-21:00 |
|
December1, 2022 |
Cohomology of nilpotent Leibniz algebras |
21:00-22:00 |
|
December2, 2022 |
Deformation cohomology of rack bialgebras |
20:00-21:00 |
|
December2, 2022 |
Deformation cohomology of rack bialgebras vs cohomology of Leibniz algebras |
21:00-22:00 |
Bio:Friedrich Wagemann, is a Professor from University of Nantes, France. He mainly studies Lie Theory and Mathematical Physics. He has published more than 40 high-level academic papers in Comm. Math. Phys., Adv. Math., Trans. Amer. Math, Soc., Pro. Lond. Math. Soc., IMRN and other journals.
Quasi-local mass and geometry of scalar curvature
Speaker:Yuguang Shi (Peking Universtiy)
Time:2022年11月25日 10:30-11:30
Meeting ID:腾讯会议:520-112-012
Abstract:Let (Σ^(n-1),γ) be an (n-1)-dimensional orientable Riemannian manifold, H be a positive function on Σ^(n-1), Gromov’s asked under what conditions γ is induced by a Riemannian metric g with nonnegative scalar curvature, for example, defined on Ω^n, and H is the mean curvature of Σ in (Ω^n,g) with respect to the outward unit normal vector? By the recent result due to P. Miao we know such H cannot be too large, so the next natural question is what is “optimal” H so that such a fill-in for the triple (Σ^(n-1),γ,H) exits? It turns out that the problem has deep relation with positive mass theorem, in this talk I will talk about some known results relate to this topic. My talk is based on my joint works with Dr. Wang Wenlong, Dr.Wei Guodong,Dr. Zhu Jintian, Dr.Liu Peng, Dr. Hu Yuhao.
Bio:史宇光,1996年在中科院数学研究所获博士学位,1997年至1999年分别于香港中文大学,北京大学数学科学学院从事博士后研究,后留北大工作。曾获得国家杰出青年基金项目资助,当选长江特聘教授,入选第二批国家“万人计划”科技创新领军人才。于2010年,获第十一届中国青年科技奖;2011年,获理论物理国际中心(ICTP)Ramanujan奖;2020年,获教育部高等学校科学研究自然科学奖一等奖。
Local derivations and automorphisms on solvable Lie algebras of maximal rank
Speaker:Bakhrom Omirov (National University of Uzbekistan)
Time:2022年11月18日 10:30-11:30
Meeting ID:ZOOM ID:862 062 0549,Code:2022
会议链接:
https://us02web.zoom.us/j/8620620549?pwd=bGhsaG15WjRza2V3ZEN4TzJYZ1FZQT09
Abstract:The present talk is devoted to the description of local derivations and automorphisms on solvable Lie algebras of maximal rank. First, we present the general form of an automorphism on solvable Lie algebra of maximal rank. Namely, any automorphism can be represented as a composition of inner, diagonal and graph automorphisms. We show that all local derivations and all local automorphisms of solvable Lie algebra of maximal rank are global, while there are examples of solvable Lie algebras of non-maximum rank with different behavior of local derivations and local automorphisms. We also apply the main results to the descriptions of local derivations and local automorphisms on standard Borel subalgebras of complex simple Lie algebras.
Bio:Bakhrom Omirov is a professor at the National University of Uzbekistan. His research focused on non-associative algebras and superalgebras. In particular, he is one of the authors of the monograph devoted to the structure theory of Leibniz algebras. Bakhrom Omirov is a member of The World Academy of Sciences, which includes 66 countries), as well as Uzbek and American Societies. He is a winner of several prestigious fellowships (Fulbright, USA; INTAS, Belgium).
On the first cohomology group of Murray-von Neumann algebras
Speaker:Karimbergen Kudaybergenov (V.I. Romanovskiy Institute of Mathematics, Uzbekistan Academy of Sciences)
Time:2022年11月18日 15:30-16:30
Meeting ID:ZOOM ID:862 062 0549,Code:2022
会议链接:
https://us02web.zoom.us/j/8620620549?pwd=bGhsaG15WjRza2V3ZEN4TzJYZ1FZQT09
Abstract:This talk presents a full resolution of the problem stated by Ayupov in 2000 and partly restated in 2014 by Kadison and Liu. We explain a background of the Ayupov–Kadison–Liu Problem and its connection with general derivation theory in operator algebras starting with fundamental results due to Kaplansky, Kadison, Sakai and others. We shall cite and brief explain major results concerning derivations on algebras of unbounded operators and list results concerning some special cases of the problem. Finally, the main result yielding the full resolution will be stated.
Bio:Karimbergen Kudaybergenov is a head at the Karakalpak branch of V.I.Romanovskiy Institute of Mathematics, Uzbekistan Academy of Sciences. His research focused on operator algebras and mappings on non-associative algebras. Karimbergen Kudaybergenov is an influential expert in the studies of derivations of unbounded operator algebras, who is also an exceptionally prolific author publishing his results in top internationally recognized journals. The highest quality of his research contributions has been recognized in Uzbekistan. In 2017, he was awarded the State Prize of the first degree in the field of Science and Technology of the Republic of Uzbekistan. Further, in 2017, he was awarded an Honored Scientist of the Republic of Karakalpakstan.
Equilibrium programming: background and some new concepts
Speaker:Boris Budak (Moscow State University)
Time:2022年11月17日 15:45-16:45,
Meeting ID:ZOOM ID:862 062 0549,Code:2022
会议链接:
https://us02web.zoom.us/j/8620620549?pwd=bGhsaG15WjRza2V3ZEN4TzJYZ1FZQT09
Abstract:Equilibrium programming is a broad area of mathematics that studies mathematical models of numerous phenomena in natural sciences and economics. A typical situation is when exact values of functional Φ(v,w) are not available when finding the numerical solution to the equilibrium programming problem and we have only their approximations. It is known that numerical models do not always work correctly in that situation, and different types of regularization must be applied. One of the best-known of these is Tikhonov’s regularization, which is usually used in processing approximate data. Some classic and new concepts of regularization will be discussed, a new regularized shooting model based on Tikhonov regularization for solving problems of equilibrium programming with inexact data will be given as an example.
Bio:Boris Budak is an associated professor of Faculty of Computational Mathematics and Cybernetics, Moscow State University. His Main Scientific Interests and Results including:
1. Extremal problems with disturbed data, optimal control, stabilization and regularization.
2. Developed and investigated a family of continuous methods for equilibrium programming problems solving, developed regularized analogues of these methods for the situation, when initial data is disturbed.
3. Created a new so-called “shooting” method for equilibrium programming problems solving, developed regularized analogue of it.
4. Solved some problems dedicated to a search of an operator with minimal norm, that guarantees a given solution of a linear operator equation in Hilbert spaces.
Complex cobordisms, the universal formal group, and theta divisors
Speaker:Victor Matveevich Buchstaber (Steklov Mathematical Institute, Russian Academy of Sciences)
Time:2022年11月11日 15:30-16:30
Meeting ID:ZOOM ID:862 062 0549,Code:2022
会议链接:
https://us02web.zoom.us/j/8620620549?pwd=bGhsaG15WjRza2V3ZEN4TzJYZ1FZQT09
Abstract: The talk is devoted to fundamental connections between algebraic topology, the formal groups theory and algebraic geometry.
The focus will be on the result of V.M. Buchstaber and A.P. Veselov, 2020. According to this result the exponent of the universal one-dimensional formal group is given by a series f(t) with the coefficient at t^{n+1}/ (n+1)! which is equal to the complex cobordism class of the theta divisor of a general (n+1)-dimensional abelian variety. We will discuss the applications of this result to well-known problems of algebraic topology and algebraic geometry, including the still open Milnor-Hirzebruch problem on the Chern numbers of irreducible smooth algebraic varieties.
The talk is designed for a wide audience, all the necessary concepts will be introduced.
Bio: Prof. Victor Matveevich Buchstaber is an expert in algebraic topology, geometric combinatorics, mathematical physics, founder of a large scientific school in topology and its applications, corresponding member of the Russian Academy of Sciences, chief scientific researcher of the Moscow Mathematical V.A.Steklov Institute, professor of the Moscow State M.V. Lomonosov University, Vice President of the Moscow Mathematical Society.
Conservative algebras
Speaker:Ivan Kaygorodov (University of Beira Interior)
Time:2022年11月04日 15:30-16:30
Meeting ID:ZOOM ID:862 062 0549,Code:2022
会议链接:
https://us02web.zoom.us/j/8620620549?pwd=bGhsaG15WjRza2V3ZEN4TzJYZ1FZQT09
Abstract: The class of conservative algebras was introduced in 1972 by I. Kantor. Roughly speaking, it is a class of algebras satisfying a "quasiidentity'' of degree 4. The class of conservative algebras includes many important varieties of algebras, such as associative algebras, Lie algebras, Leibniz algebras, Zinbiel algebras, Jordan algebras, etc. Conservative algebras and superalgebras have some similar properties to many well-known varieties of algebras. For example, they admit the Tits-Koecher-Kantor construction (TKK construction); each conservative algebra (and superalgebra) could be embedded in a suitable universal conservative algebra (or superalgebra). We will talk about some old and new results from this topic.
Bio: Ivan Kaygorodov got his Ph.D. in 2010 at the Sobolev Institute of Mathematics (Russia). He has worked as a postdoctoral researcher at the University of Sao Paulo (Brazil) and as an assistant professor at the Federal University of ABC (Brazil) for 10 years. Now he is a research fellow at the University of Beira Interior (Covilhã, Portugal). He is the Editor-in-Chief of Communications in Mathematics. His main area of research interest is in non-associative algebras.
Weak Leibniz algebras and transposed Poisson algebras
Speaker:Askar Jumadildayev (Kazakh-British Technical University)
Time:2022年10月28日 14:00-15:00
Meeting ID:ZOOM ID:862 062 0549,Code:2022
会议链接:
https://us02web.zoom.us/j/8620620549?pwd=bGhsaG15WjRza2V3ZEN4TzJYZ1FZQT09
Abstract: Weak Leibniz algebras are defined by the following identities: $[a,b]c=2(a(bc)-b(ac))$ and $a[b,c]=2((ab)c-(ac)b).$ Any two-sided Leibniz algebra, in particular any Lie algebra is weak Leibniz. We show that polarization of any weak Leibniz algebra is transposed Poisson and conversely, depolarization of any transposed Poisson algebra is weak Leibniz. Well known that any simple Leibniz algebra is Lie. We construct simple weak Leibniz algebras that are not Lie.
Bio: Askar Jumadildayev is a professor of Kazakh-British Technical University. His research interests concern cohomologies and deformations of Lie algebras, N-commutators of vector fields, identities of non-associative algebras and operads theory.
SU-bordism: geometric representatives, operations, multiplications and projections
Speaker:Panov Taras (Moscow State University)
Time:2022年10月21日 15:00-16:00
Meeting ID:ZOOM ID:862 062 0549,Code:2022
会议链接:
https://us02web.zoom.us/j/8620620549?pwd=bGhsaG15WjRza2V3ZEN4TzJYZ1FZQT09
Abstract: The development of algebraic topology in the 1960s culminated in the description of the special unitary bordism ring. Most leading topologists of the time contributed to this result, which combined the classical geometric methods of Conner-Floyd, Wall and Stong with the Adams-Novikov spectral sequence and formal group law techniques that emerged after the fundamental 1967 work of Novikov.
Thanks to toric topology, a new geometric approach to calculations with SU-bordism has emerged, which is based on representing generators of the SU-bordism ring and other important SU-bordism classes by quasitoric manifolds and Calabi-Yau hypersurfaces in toric varieties.
We shall also discuss more specific topics related to SU-bordism. Namely we show that SU-linear operations in complex cobordism are generated by the well-known geometrical operations $\partial_i$. For the theory $W$ of $c_1$-spherical bordism, we describe SU-linear multiplications on W and projections $MU \to W$. We also analyse complex orientations on $W$ and prove results on the s-numbers of the coefficients of the corresponding formal group laws.
The talk is based on joint work with Zhi Lu, Ivan Limonchenko and Georgy Chernykh.
Bio: Panov Taras,Professor, Faculty of Mathematics and Mechanics, Moscow State University; Moscow Mathematical Society prize (2004); Shuvalov Prize of Moscow University (2010).
Personal Web Page: http://higeom.math.msu.su/people/taras/english.html.
Properties of polynomial maps and two-dimensional Jacobian conjecture
Speaker:Yucai Su (Tongji University)
Time:2022年10月14日 14:30-15:30 Beijing time
Meeting ID:ZOOM ID:862 062 0549,Code:2022
会议链接:
https://us02web.zoom.us/j/8620620549?pwd=bGhsaG15WjRza2V3ZEN4TzJYZ1FZQT09
Abstract: For any two polynomials on two variables with a nonzero Jacobian determinant, there corresponds a polynomial map known as a Keller map. In this talk, the speaker will report 3 properties of Keller maps, which are used to give a proof of the two-dimensional Jacobian conjecture in the speaker’s paper entitled ``a proof of 2-dimensional Jacobian conjecture'' at arXiv:1603.01867.
Bio: Yucai Su is a professor at Tongji University and Jimei University. He has successively worked as a visiting scholar and postdoctoral researcher at Queen Mary and Westfield College, the University of London, Concordia University, and the University of Quebec at Montreal for 7 years. His main research interests include Lie algebras, representation theory and Jacobian problem. In particular, he has studied the Jacobian Conjecture for eighteen years. He is an editor of Algebra Colloquium and Journal of Mathematical Study, and published over 100 papers in Adv. Math., J. Eur. Math. Soc., Proc. London Math. Soc., Comm. Math. Phys., Math. Z., Israel J. Math., etc. Recently, using the local bijectivity of Keller maps, he solved the 2-dimensional Jacobian Conjecture.
FROM OPERADS TO OPERADIC CATEGORIES
Speaker:Michael Batanin (Institute of Mathematics of Czech Academy of Science, Charles University, Prague)
Time:2022年09月30日 16:30-17:30
Meeting ID:ZOOM ID:862 062 0549,Code:2022
会议链接:
https://us02web.zoom.us/j/8620620549?pwd=bGhsaG15WjRza2V3ZEN4TzJYZ1FZQT09
Abstract: Operads were introduced at the end of 1960s by Boardman, Vogt and P.May as spaces parametrising multivariable operations and their substitutions. In the 1990's however, it was realised that there are other interesting types of operads such as cyclic and modular operads of Getzler and Kapranov (motivated by TQFT development) and globular n-operads of Batanin parametrising higher categorical compositional structures. In 2015 Batanin and Markl introduced operadic categories in order to develop a consistent theory of operadic like structures. In my talk I explain what operadic category and associated category of operads are and why this is a very rich and useful new algebraic concept.
Bio: The speaker graduated from Novosibisk State University in 1983. He is currently a Senior Researcher at the Institute of Mathematics of Czech Republic, and a Professor of Charles University in Prague. He is specialising in Algebraic Topology, Category Theory, Operads and related topics.
International Frontiers of Mathematics
Zoom ID: 862 062 0549 Password: 2022

孤立波:1834-1984
Speaker:张大军 上海大学
Time:2022年09月23日 10:30-11:30
Meeting ID:腾讯会议:309-266-962
腾讯会议链接:https://meeting.tencent.com/dm/jx2ianwNTLKT
Abstract: 这是一个关于“孤立波”的历史与发展的科普报告。1834年 John Scott Russell首次发现孤立波,1895年Korteweg和de Vries (KdV) 利用KdV方程描述了孤立波现象, 1965年 Kruskal 和 Zabusky在研究Fermi-Pasta-Ulam问题时发现并命名了“soliton” (孤立子), 两年以后Gardner-Greene-Kruskal-Miura 建立了反散射方法(Inverse Scattering Transform), 成为现代可积理论的起点。报告将回顾孤立波与可积系统在前150年(1834-1984)的历史,回顾期间(特别是1968-1984)出现的重要的可积模型以及重要的理论与方法进展。
Bio: 张大军,上海大学数学系教授,博士生导师。主要从事离散可积系统与数学物理的研究,包括离散可积系统的直接方法、多维相容性的应用、空间离散下的可积结构与连续对应等。曾访问Turku大学、Leeds大学、剑桥牛顿数学研究所、Sydney大学等学术机构。先后主持国家自然科学基金面上项目5项。目前担任离散可积系统国际系列会议SIDE (Symmetries and Integrability of Difference Equations)指导委员会委员(2012-)和国际期刊Journal of Physics A编委(2020-)。
Coarse geometry and operator algebras : a minicourse
Speaker:Yeong Chyuan Chung 博士后 Leiden University
Meeting ID:腾讯会议:869-2118-6000,密码:3721
腾讯会议链接:https://meeting.tencent.com/dm/x708itdk0Eq1
Abstract: Coarse geometry involves studying metric spaces by looking at them from far away, and it is important in areas of mathematics such as geometric group theory. In recent times, its interaction with operator algebras has also been an active area of research with applications to problems in topology and differential geometry. In this mini-course, we aim to introduce basic notions in coarse geometry and a class of operator algebras known as Roe algebras. Starting from coarse geometry, we will introduce basic definitions such as coarse embeddings and coarse equivalences, then we will introduce some coarse geometric invariants such as asymptotic dimension and property A. Next, we will introduce Banach algebras and C*-algebras with examples of these, then we will focus on Roe algebras and how they reflect the coarse geometry of the underlying metric spaces. Finally, we will briefly introduce operator K-theory and the coarse Baum-Connes conjecture involving the K-theory of Roe algebras.
|
授课日期 Date of Lecture |
课程名称(讲座题目) Name (Title) of Lecture
|
授课时间 Duration |
参与人数 Number of Participants |
|
Sep 19, 2022 |
Introduction to coarse geometry: basic definitions and asymptotic dimension |
19:30-20:30 |
30 |
|
Sep 20, 2022 |
Introduction to coarse geometry: property A |
19:30-20:30 |
30 |
|
Sep 21, 2022 |
Banach algebras and C*-algebras with examples |
19:30-20:30 |
30 |
|
Sep 22, 2022 |
Roe algebras I |
19:30-20:30 |
30 |
|
Sep 26, 2022 |
Roe algebras II |
19:30-20:30 |
30 |
|
Sep 27, 2022 |
Basic operator K-theory |
19:30-20:30 |
30 |
|
Sep 28, 2022 |
K-theory of Roe algebras and the coarse Baum-Connes conjecture |
19:30-20:30 |
30 |
|
Sep 29, 2022 |
A quick look at a counterexample to the coarse Baum-Connes conjecture |
19:30-20:30 |
30 |
Bio: Yeong Chyuan Chung(钟永权),2017年博士毕业于美国德州农工大学, 主要从事粗几何、L^p算子代数、K-理论的研究。 近年来在J. Funct. Anal.,J. Noncommut. Geom.等杂志上发表多篇高水平论文。
Advanced Numerical Methods with Applications
Speaker:Andrey Dorogovtsev professor(Institute of Mathematics,NAS Ukraine)
Meeting ID:Zoom会议 ID:会议号:852 4434 8793,密码:075030
Abstract: This course aims to provide a solid introduction on some advanced numerical methods and its applications. The first part of the course will introduce the definition of local times and Gaussian functionals, then discuss some properties when local times as a Gaussian functionals. And the second part of the course is devoted to introduce Hausdorff measure and dimension, then use the Hausdorff measure and dimension to discuss sef-intersections set of Brownian motion. Professor Andrey will give students some time to understand the knowledge and give some small questions about the lecture.
|
授课日期 Date of Lecture |
课程名称(讲座题目) Name (Title) of Lecture |
授课时间 Duration (Beijing Time) |
参与人数 Number of Participants |
|
2022-09-19 |
Local times and sets of values of random fields |
16:00-17:00 |
30 |
|
2022-09-21 |
Gaussian white noise and functionals from it |
16:00-17:00 |
30 |
|
2022-09-26 |
Local times as a Gaussian functionals |
16:00-17:00 |
30 |
|
2022-09-28 |
Local nondeterminism for Gaussian random fields |
16:00-17:00 |
30 |
|
2022-10-03 |
Hausdorff measure and dimension |
16:00-17:00 |
30 |
|
2022-10-05 |
Haussdorf dimension for sef-intersections set of Brownian motion |
16:00-17:00 |
30 |
Bio: Andrey Dorogovtsev教授是乌克兰国家科学院通讯院士,乌克兰国家科学院数学所随机过程理论系主任,主要从事概率论及其相关领域研究,是乌克兰概率论研究方向学术领军人物之一。Andrey Dorogovtsev教授是乌克兰与德国、乌克兰与俄罗斯等国家联合项目的乌方负责人。同时,Andrey Dorogovtsev教授是《Theory of Stochastic Processes》、《Ukraine Mathematical Journal》等杂志的编委。
Noncommutative differential geometry and quantum effects of gravity
Speaker:张晓(中国科学院数学与系统科学研究院)
Time:2022年09月16日 10:30-11:30
Meeting ID:腾讯会议 ID:602-653-169
点击链接入会:https://meeting.tencent.com/dm/7TgVgfHRMj51
Abstract: We provide a rigorous theory of noncommutative metrics and curvatures in frame of deformation quantization. In terms of them, we are able to propose the noncommutative Einstein field equations. We show that the deformation of classical pp-waves are exact solutions of vacuum field equations. We also find that the quantization of spherically symmetric metrics is renormalizable and the deformation of classical Schwarzschild solution is the quantum black hole solution which does not depend on time and can not be evaporated. The talk is based on the early joint works with Chaichian, Tureanu, D. Wang, R.B. Zhang as well as H. Gao recently.
Bio: 张晓,中国科学院数学与系统科学研究院数学研究所研究员,国家杰出青年基金及中科院百人计划获得者。现任广西大学君武学者和广西八桂学者,广西数学研究中心执行主任。从事广义相对论的数学研究,在广义相对论正能量问题及引力量子化的非交换几何理论上作出了系统性的贡献。
Higher algebraic structures-a minicourse
Speaker:Camilo Andres Angulo Santacruz(Universidade Federal Fluminense)
Meeting ID:ZOOM ID:862 062 0549 Password:2022
点击链接入会:
https://zoom.us/j/8620620549?pwd=bGhsaG15WjRza2V3ZEN4TzJYZ1FZQT09
Course Abstract:“Higher structure” is a term used loosely to refer to a large collection of structures that share a common theme. Suppose a mathematical structure consists of a collection of sets, functions between them, and some equations that the latter shall verify. Think of group structures, for instance, as the sets G, GxG, and the singleton, together with three functions (the multiplication, the unit, and the inverse) that verify the usual axioms of a group, which are equations relating them(!). The common idea behind higher structures is that they roughly are like mathematical structures, but replacing sets by homotopy types, equations by homotopies, and adding higher-order homotopies to enforce coherence.
Higher structures have an intricate history and abound in mathematics. We will focus on three types of higher structures that have algebraic flavor.In what follows we describe the plan of the lectures. We will start by giving a bit of a panoramic perspective on the history and emergence of the higher structures we will consider. After going through some preliminaries, we proceed to study them one by one, starting with the so-called L-infinity algebras, continuing with stacky groupoids, and closing with Lie n-groupoids. In each module, we go through definitions, examples, and main constructions. We conclude by trying and relating these structures among them and by giving an outlook for the directions in which these generalize by touching upon some recent research topics.
Bio:Camilo Andres Angulo Santacruz is a post doctor from Universidade Federal Fluminense, Brazil. He mainly study Poisson geometry and higher structures.
怪波/畸形波简介
Speaker:闫振亚(中科院数学院系统所)
Time:2022年09月09日 10:30-11:30
Meeting ID:腾讯会议 ID:737-700-086
点击链接入会:https://meeting.tencent.com/dm/VWCgdy2stinj
Abstract: 不同于通常的孤子(soliton), 怪波(rogue wave/rogon)拥有巨大的能量,也被称为畸形波、巨波、极端波等。它最早出现在深水海洋中,后来人们发现很多自然科学中也存在怪波现象,如光学、Bose-Einstein凝聚态、等离子体物理、大气科学、生物学和金融市场等。从某种意义来说,社会科学中的突发问题也属于怪波范畴。本报告介绍线性和非线性科学问题中怪波的背景、发展和挑战等。另外讨论怪波产生的一些物理机理等。
Bio: 闫振亚,中科院数学院系统所研究员,主要研究可积系统理论、怪波、PT对称、智能数学物理及交叉应用等。2019年获得国家自然科学基金杰出青年基金。
Operators on the universal enveloping algebras and quantisation of the argument shift method
Speaker:Georgy Sharygin(Lomonosov Moscow State University)
Time:2022年09月09日 21:00-22:00
Meeting ID:ZOOM ID:862 062 0549 Password:2022
点击链接入会:
https://zoom.us/j/8620620549?pwd=bGhsaG15WjRza2V3ZEN4TzJYZ1FZQT09
Abstract: Argument shift method is an important and simple method to generate large commutative subalgebras in Poisson algebras, in particular in the algebras of functions on coadjoint representation of a Lie algebra. In the last 20 years a considerable in finding "quantized version" of such algebras was achieved: in the papers of Rybnikov, Molev and others one can find many examples of commutative subalgebras in the universal enveloping algebras of different Lie algebras, that "raise" the subalgebras, obtained by the argument shift method. However these subalgebras are constructed by "quantizing" concrete sets of generators in the "classical" argument shift subalgebras, and no general construction of "shifting" in the universal enveloping algebras is known. In my talk I will discuss a potential "quantum counterpart" of the shift in a particular case of the Lie algebra gl_n. It is based on the use of "quasi-derivations" of Ugl_n, introduced by Gourevitch and Saponov. I will describe these operators and discuss their relation with other constructions. I will also discuss the experimental data that supports the conjecture that one can define the quantum shift of the argument using these operators.
Bio: Georgy Sharygin got his PhD from Moscow State University in 2000, and since that time he has been teaching Mathematics at all levels from High school to the PhD programs. He was invited speaker at many international conferences, was many times invited researcher in various international institutes. His research interests include deformation quantisation, non commutative geometry, topology, differential geometry and integrable systems.
The category of 2D rational CFT's
Speaker:孔良(南方科技大学)
Time:2022年09月02日 21:00-22:00
Meeting ID:腾讯会议 ID:939-656-494
点击链接入会:https://meeting.tencent.com/dm/aTqabg1ACJK5
Abstract: In this talk, I will review the categorical study of 2D rational CFT's and topological defects in the last two decades. In the end, I will show how to use it to describe the category of 2D rational CFT's.
Bio: 孔良,南方科技大学深圳量子科学与工程研究院研究员。1994年于中国科学技术大学获得物理学士学位,2005年于美国Rutgers,the State University of New Jersey获得数学博士学位。主要研究拓扑量子场论和共形场论的数学理论,以及在拓扑物质态中的应用。
可积系统中的Darboux变换简介
Speaker:刘青平(中国矿业大学)
Time:2022年08月19日 10:00-11:00
Meeting ID:腾讯会议 ID:721-493-311
点击链接入会:https://meeting.tencent.com/dm/BnT3kqNexgYQ
Abstract: 这是关于Darboux变换的一个科普报告。我们将从Jean Gaston Darboux发表于1882年一篇短文谈起,介绍什么是Darboux变换、构造Darboux变换的方法以及它在可积系统理论中的应用。
Bio: 刘青平,国务院政府特殊津贴获得者,北京市高等学校教学名师,1992年获英国Leeds大学博士学位,曾在中国科学院理论物理研究所和西班牙Complutense大学做博士后,现为中国矿业大学(北京)教授。从事可积系统理论及其应用研究。更多信息见个人主页:https://lxy.cumtb.edu.cn/info/1067/1238.htm
Morse指标定理简介
Speaker:胡锡俊(山东大学)
Time:2022年08月12日 10:00-12: 00
Meeting ID:腾讯会议 ID:324-276-209
点击链接入会:https://meeting.tencent.com/dm/syKSSjFXHH5R
Abstract: Morse指标定理源于对测地线的研究,它将Morse指标表为测地线共轭点的重数之和。在本次演讲中我们将回顾Morse指标定理的经典结论并介绍最新的进展。
Bio: 胡锡俊,山东大学教授。1997年7月和1999年7月在吉林大学分别获得学士学位和硕士学位,2002年7月在南开大学获得博士学位。2014年获得国家杰出青年基金,主要研究方向为哈密顿系统与非线性分析。在天体力学中周期解的稳定性问题,哈密顿系统指标理论及一类反应-扩散方程行波解的研究中做出了创新性的工作。
Symmetries: from groups to tensor categories
Speaker:Alexei Davydov(Ohio University)
Time:2022年08月12日 16:00-17: 00
Meeting ID:ZOOM ID:862 062 0549, Password:2022
点击链接入会:
https://us02web.zoom.us/j/8620620549?pwd=bGhsaG15WjRza2V3ZEN4TzJYZ1FZQT09
Abstract: Groups are mathematical ways of talking about symmetries. From its beginning Group Theory was driven by the idea of symmetry and its applications (e.g. Galois' proof of unsolvability of a quintic). One of the most spectacular applications of Group Theory was the classification of crystals done at the end of the 19th century. In the middle of the 20th century Group Theory was used to describe all known states of matter. Experimental developments of the condensed matter physics at the end of the 20th century were not fitting the standard Group Theory scheme. They forced us to generalize the mathematical formulation of symmetry. The talk will be about this generalized notion, the one of tensor category.
Bio: Alexei Davydov is a Professor of Department of Mathematics, Ohio University. He mainly works on category theory and homological algebra.
Gravity properad, moduli spaces M_g,n, and string topology
Speaker:Sergei Merkulov University of Luxembourg
Time:2022年08月05日 16:00-18: 00
Meeting ID:ZOOM ID:862 062 0549
Password:2022
点击链接入会:
https://us02web.zoom.us/j/8620620549?pwd=bGhsaG15WjRza2V3ZEN4TzJYZ1FZQT09
Abstract: Using Thomas Willwacher’s twisting endofunctor, and Kevin Costello’s theory of partially compactified moduli spaces of algebraic curves of arbitrary genus with marked points, we introduce a new dg properad which contains Ezra Getzler’s operad controlling genus zero moduli spaces. We discuss its applications in the theory of moduli spaces M_g,n, and in string topology.
Bio: Sergei Merkulov is a Professor at the University of Luxembourg. He worked previously at the Russian Academy of Sciences, the Glasgow University (UK) and the Stockholm University (Sweden). He works on category theory, homological algebra and Differential geometry.
Thick morphisms of supermanifolds and homotopy algebras
Speaker:Theodore Voronov University of Manchester
Time:2022年07月29日 16:00-18: 00
Meeting ID:ZOOM ID:862 062 0549
password:2022
点击链接入会:
https://us02web.zoom.us/j/8620620549?pwd=bGhsaG15WjRza2V3ZEN4TzJYZ1FZQT09
Abstract: Supergeometry can be used as a unifying language for many algebraic and differential-geometric constructions. Particular role here is played by homological vector fields, i.e. odd vector fields Q satisfying Q^2=0. They can be useful for describing “higher” or “homotopy” analogs of Poisson brackets. Recently I discovered a generalization of the notion of a smooth map (called by me “thick morphisms”) giving NONLINEAR pullbacks on smooth functions. “Thick morphisms” can in particular provide L_infinity morphisms for homotopy Poisson structures. There are other interesting connections, e.g. with Fourier integral operators. Thick morphisms also provide a nonlinear analog of classical functional-algebraic duality.
Bio: Dr Theodore Voronov is a Professor in Pure Mathematics at the University of Manchester (UK). His research interests are on the crossroads of algebra, differential geometry, topology and mathematical physics; in particular, geometry of supermanifolds and its applications. See more at
http://personalpages.manchester.ac.uk/staff/theodore.voronov.
Representations of the Fermion-Virasoro algebras
Speaker:赵开明 Wilfrid Laurier University
Time:2022年07月15日 09:00-11:00
Meeting ID:
腾讯会议 ID:635-613-814
点击链接入会,或添加至会议列表:
https://meeting.tencent.com/dm/aEOWDPUh24oM
Abstract: We introduce Fermion algebras F and the Fermion-Virasoro algebras. They are infinite-dimensional Lie superalgebras. The progress on simple smooth modules and simple Harish-Chandra modules over these algebras will be discussed.
Bio: 赵开明,加拿大Wilfrid Laurier大学教授,主要研究方向为李代数。主持多项国家自然科学基金, 及加拿大NSERC基金。他在 Adv. Math., Tran. AMS, J. Lond. Math. Soc., J. Algebra 等国际刊物上发表学术论文100多篇。
Rota-Baxter bisystems and mixed bialgebras
Speaker:Abdenacer Makhlouf(Université de Haute Alsace)
Time:2022年07月08日 16:00-17:00
Meeting ID:
ZOOM ID:862 062 0549,Code:2022
会议链接:
https://us02web.zoom.us/j/8620620549?pwd=bGhsaG15WjRza2V3ZEN4TzJYZ1FZQT09
Abstract: In this talk, we deal with a generalization of the concept of Rota-Baxter operators defined by T. Brzezi´nski and called Rota-Baxter systems which appeared in [J. Algebra 460(2016):1- 25]. We provide a dual version and then consider a generalization to bialgebras, we introduce the notion of Rota-Baxter bisystem and construct various examples. On the other hand, we introduce a new type of bialgebras (named mixed bialgebras) which are consisting of an associative algebra and a coassociative coalgebra satisfying the compatible condition determined by two coderivations. We investigate coquasitriangular mixed bialgebras and the particular case of coquasitriangular infinitesimal bialgebras, where we give the double construction. This is a joint work with Tianshui Ma and Sergei Silvestrov.
Bio: Abdenacer Makhlouf is a Professor and the head of Mathematics Department at University of Haute Alsace, Mulhouse, France. His research covers structure, representation theory, deformation theory and cohomology of various types of algebras, including Nonassociative algebras, Hopf algebras and n-ary algebras.
Kahler-Ricci flow on smooth minimal models
Speaker:张振雷(首都师范大学)
Time:2022年07月01日 10:00-12:00
Meeting ID:腾讯会议 ID:780-765-137
To Join Tencent Meeting: https://meeting.tencent.com/dm/5cjuobQFgOpb
Abstract: It is a survey talk on the long-time behavior of a Kahler-Ricci flow on a smooth manifold with a semi-ample canonical line bundle.
Bio:张振雷,首都师范大学数学科学学院教授。2003年本科毕业于吉林大学数学科学学院;2008年博士毕业于南开大学陈省身数学研究所,导师方复全教授。2018年获国家自然科学基金杰出青年科学基金资助,主要研究Ricci流、Kahler-Ricci流。
奇妙的基础数学
Speaker:徐晓平(中国科学院大学)
Time:2022年06月24日 14:00-16:00
Meeting ID:腾讯会议 ID:703-956-224
To Join Tencent Meeting: https://meeting.tencent.com/dm/gtlAO1KvxQLo
Abstract:这是一个科普型报告。我们从“什么是数学”谈起。然后是:素数的故事,拉马驽金的故事,分隔函数,KdV方程,量子物理的基本数学模型。之后,我们讲:数学的残缺美,一些挑战性问题以及本人的一些研究体验。
Bio:徐晓平,中国科学院大学教授,中国科学院数学研究所所长。1992年在美国Rutgers大学取得博士学位,师从著名的李理论专家James Lepowsky 和Robert Lee Wilson。之后在香港科技大学工作十年。2002年回到中国科学院数学研究所工作, 2014年开始兼任中国科学院大学教授,自2022年3月起,任中国科学院数学研究所所长。获宝钢优秀教师奖。他在李代数、顶点算子代数(共形场论)和偏微分方程的代数解法等相关领域的研究中做出了重要贡献。
低维拓扑学的世纪回顾
Speaker:雷逢春(大连理工大学)
Time:2022年06月24日 10:00-12:00
Meeting ID:685-963-603
To Join Tencent Meeting: https://meeting.tencent.com/dm/49Yn9DtKVB4q
Abstract:拓扑学是当代核心数学的一个重要前沿领域,其渊源可追溯到欧拉早期的工作(1836年,哥尼斯堡七桥问题的解答)。拓扑学奠基于19世纪末, 在20世纪取得了梦幻般的发展, 进入21世纪更加兴旺发达。本报告将对拓扑学的发展作一个跨越世纪的通俗概要浏览, 重点介绍低维拓扑学的发展,即二、三和四维流形拓扑学的主要成就。
Bio:雷逢春,1990年12月博士毕业于吉林大学基础数学专业,研究方向为低维拓扑,现为大连理工大学数学科学学院教授、博士生导师。长期从事三维流形拓扑方面的研究工作,多次承担国家自然科学基金面上项目、重点项目和海外及港澳学者合作研究基金(延续)项目的研究工作。曾于1997年荣获国家教委科技进步二等奖(排名3),2001年获黑龙江省杰出青年科学基金,2002年入选教育部“跨世纪优秀人才培养计划”。现为中国数学会常务理事,辽宁省数学会副理事长,大连市数学学会理事长。
Factorization of Shapovalov elements
Speaker:Andrey Mudrov(Moscow Institute of Physics and Technology and University of Leicester)
Time:2022年06月17日 15:00-17: 00
Meeting ID:ZOOM ID:862 062 0549, Password:2022
Abstract:A classical result of J. Bernstein, I. Gelfand and S. Gelfand says that a singular vector in a Verma module over a simple complex Lie algebra can be obtained from its highest vector by applying a product of special elements of the negative nilpotent subalgebra called Shapovalov elements. We provide explicit formulas for those elements, and hence for singular vectors of the Verma modules, expressing them through certain matrix elements of the inverse contravariant Shapovalov form.
Bio:The speaker is currently an Associate Professor and a Senior Researcher at the Center of Fundamental Mathematics in MIPT, and an Honorary Lecturer at the University of Leicester. He is specializing in quantum groups, deformation quantization and related topics.
关于最对称的双曲环面上的闭测地线
Speaker:张影(苏州大学)
Time:2022年06月10日 10:00-12:00
Meeting ID:564-626-700
To Join Tencent Meeting:https://meeting.tencent.com/dm/p7VBNfhblItm
Abstract:在与李祥飞的合作工作中,我们研究具有最大对称性的完备的双曲环面上的闭测地线的性质,证明一般闭测地线的迹多项式的正性,一些简单闭测地线长度的单调性,并提出简单闭测地线的迹的凸性猜测,以及一般闭测地线的迹多项式系数的对数凹性猜测。
Bio:张影,1985.9-1999.5 吉林大学数学系本研学习、任教,1999.5-2004.7 新加坡国立大学读研,2006.3-2007.2 巴西国家数学所(IMPA)博士后,2009.6至今,苏州大学数学科学学院教授。从事几何拓扑学研究。
同调论简史
Speaker:段海豹 (中国科学院数学与系统科学研究院)
Time:2022年5月27日 10:00-12:00
Meeting ID:899-680-387
To Join Tencent Meeting:meeting.tencent.com/dm/Il9TkCVA4hAL
Abstract:同调论是20世纪数学所诞生的一项新技术,是当代几何、拓扑、分析学的有力工具。报告通过 Riemann, Poincare, Brouwer, Hopf 等开拓者们的相关工作介绍,回顾同调论的背景、起源、以及发展历程。
Bio:段海豹,中国科学院数学与系统科学研究院研究员,1977年3月-1985年1月,在吉林大学数学系学习,获理学学士、硕士学位;1987年7月,在北京大学获博士学位。从事代数拓扑,微分拓扑和代数几何的教学、研究工作。 他在2005年获中国数学会陈省身数学奖,2010年获国家自然科学二等奖。
Lie 2-algebras from geometric structures
Speaker:Zhangju LIU
Time:2022.5.13 14:00-16:00
Meeting ID:347-371-151
To Join Tencent Meeting:https://meeting.tencent.com/dm/rx9v5zMU7xnV
Abstract:The notion of Lie 2-algebras is introduced as categorification of Lie algebras, Which is one of the fundamental objects in higher Lie theory and has close connection with strongly homotopy Lie algebras. The Lie 2-algebra structure has enjoyed significant applications in both geometry and mathematical physics. Strict Lie 2-algebras are equivalent to Lie algebra crossed modules, which are classified by the third cohomology of a Lie algebra.
In this talk, we’ll review several Lie 2-algebras that come from geometric structures, namely, 2-plectic manifolds; Courant algebroids; homotopy Poisson manifolds and affine structures on Lie groupoids. A 2-plectic structure on a manifold is a nondegenerate closed 3-form. There is a Lie 2-algebra structure on functions and Hamiltonian 1-forms of a 2-plectic manifold A Courant algebroid is a vector bundle together with a bilinear form, a skew-symmetric bracket and an anchor map. The bracket satisfies the Jacobi identity up to a coboundary, which generates a Lie 2-algebra on the section space of the bundle and functions on the base manifold. Parallel to the fact that there is a one-to-one correspondence between Lie algebra structures on a vector space and linear Poisson structures on the dual space, there is a one-to-one correspondence between Lie 2-algebra structures on a 2-vector space and linear homotopy Poisson structures on the dual 2-vector space. On a Lie groupoid, vector fields that are compatible with the groupoid multiplication are called multiplicative. Multiplicative vector fields with the Schouten bracket form a Lie algebra, which is not invariant under the Morita equivalence of Lie groupoids. To define vector fields on a differentiable stack, one needs to extend the Lie algebra to a Lie 2-algebra formed by affine vector fields on a Lie groupoid, which is Morita invariant.
Bio:刘张炬,北京大学/河南大学教授,1982年1月本科毕业于吉林大学,1986年6月在北京大学获得博士学位。1999年获得国家杰出青年基金。主要从事数学物理、Poisson几何等领域的研究。曾入选教育部跨世纪优秀人才支持计划,2004年获得教育部自然科学一等奖。
Morse matching method for conformal cohomology
Speaker:Pavel Kolesnikov (Sobolev Institute of Mathematics)
Time:2022.5.6 10:00-12:00
Meeting ID:862 062 0549
Password:2022
To Join Zoom Meeting:https://us02web.zoom.us/j/8620620549?pwd=bGhsaG15WjRza2V3ZEN4TzJYZ1FZQT09
Abstract:We will observe the matching method in the algebraic discrete Morse theory which provides us a powerful tool for finding Anick resolutions for associative algebras defined by generators and relations. We apply this method to find reduced Hochschild cohomologies of associative conformal algebras in order to study their relations with the cohomologies of Lie conformal algebras. In particular, we evaluate the Hochschild cohomology groups for the universal associative envelope U(3) of the Virasoro Lie conformal algebra.
Bio:Pavel Kolesnikov got his PhD in 2002 in Novosibirsk State University (NSU) and joined Sobolev Institute of Mathematics. Now he is a research fellow of the Institute and professor in the NSU. His main area of research interests is in the structure and combinatorial theory of associative and non-associative algebras, conformal and vertex algebras.
On the cobar-construction for non-simply connected spaces
Speaker:Andrey Lazarev ( Lancaster University )
Time:2022.04.22 16:00-18:00
Meeting ID:862 062 0549
Password:2022
To Join Zoom Meeting:https://us02web.zoom.us/j/8620620549?pwd=bGhsaG15WjRza2V3ZEN4TzJYZ1FZQT09
Abstract:The cobar-construction produces a differential graded (dg) algebra out of a dg coalgebra. When applied to the coalgebra of simplicial chains on a simply-connected space X, the resulting dg algebra models the chain algebra on the based loop space of X. This is a classical result of Adams and it has been known for over 60 years. In a recent breakthrough development, American mathematicians Rivera and Zeinalian removed the simple-connectivity assumption. In this talk, I will explain Rivera-Zeinalian’s result, discuss its generalizations and connections with infinity-categories.
Bio:Andrey Lazarev is a professor of pure mathematics in the University of Lancaster. His recent research deals with homotopy theory of differential graded algebras and categories, derived categories and higher phenomena. It has applications in rational homotopy theory, theory of operads and operadic algebras, algebraic topology and pure algebra. Andrey Lazarev is the Managing Editor of the journal《Bulletin of the London Mathematical Society》, as well as a Member of the Editorial Board of the journal《Higher_Structures》.
Boson-Fermion Correspondence and Its Applications to Integrable Hierarchies Revisited From The Point of View of Representation Theory and Random Walks
Speaker:Jian Zhou
Time:2022.04.15 10:00-12:00
Meeting ID:694-475-243
To Join Tencent Meetinghttps://meeting.tencent.com/dm/dbl4pDJLd3zS
Abstract:We revisit the boson-fermion correspondence and its applications to integrable hierarchies via representation theory of symmetric groups. This makes it natural to consider random walks on various diagrams and graphs related to symmetric groups. Random partitions, hypergeometric tau-functions and weighted Hurwitz numbers are then brought together under a unified probabilistic treatment, rooted in their connections to the fermionic Fock space. Various approaches to the representation theory of symmetric groups all turn out to be useful in this treatment. They include: the new approach of Okounkov and Vershik, the Hopf algebra approach of Zelevinsky, and the lambda-ring approach of Knutson. A connection to the interpolating statistics in the study of fractional quantum Hall effect will also be explained.
Bio:周坚,清华大学数学科学系教授,2005年国家杰出青年基金获得者、2009年入选国家“百千万人才工程”。他的研究领域为黎曼面的模空间与霍奇积分,拓扑场论,微分几何,弦理论等。周坚教授通过对超弦理论中Vafa学派的工作中出现的一些数学问题的研究,揭示了一些不同的数学分支之间的内在联系,他与合作者完成的“Marino-Vafa猜想的证明”入选2004年度“中国高校十大科技进展”。
Heegaard splitting: a survey
Speaker: 邱瑞锋 (华东师范大学)
Time:2022年04月08日 10:00-12:00
Meeting:#腾讯会议:680-593-921
https://meeting.tencent.com/dm/lxemeq0TOyx1
Abstract: Heegaard分解是紧致三维流形上普遍存在的组合拓扑结构,在三维流形理论的研究中起到了重要的作用。吉林大学是我国最早从事这一领域研究的研究群体,并直接或间接地培养了一批这一领域的专家学者。这个报告将介绍这一领域的国内外发展历史及现状。
Bio:邱瑞锋,华东师范大学教授,主要从事三维流形及纽结理论的研究,代表性工作有:(1)证明了Heegaard分解理论中的Gordon猜想,(2)构造了纽结洞数理论中的Morimoto猜想的反例等。
Orbifold theory and modular extensions
Speaker: 董崇英 美国加州大学Santa Cruz 分校
Time:2022-03-25 10:00-12:00
Abstract: Orbifold theory studies a vertex operator algebra V under the action of a finite automorphism group G. The main objective is to understand the module category of fixed point vertex operator subalgebra V^G. We prove a conjecture by Dijkgraaf-Pasquier-Roche on V^G- module category if V is holomorphic. We also establish a connection between rational orbifold theory and minimal modular extensions. Our work is based on the previous results on modular extensions by Drinfeld-Gelaki-Nikshych-Ostrik and Lan-Kong-Wen. This is a joint work with Richard Ng and Li Ren.
Bio: 董崇英,美国加州大学Santa Cruz分校终身教授,国际上无限维李代数和顶点算子代数领域最杰出的数学家之一,多年来一直从事无穷维李代数、顶点算子代数、Orbifold理论以及广义月光等方面的研究。在Acta Math.、Duke Math. J.、Adv. Math.、Comm. Math. Phys.等国际著名期刊发表论文100多篇,总引用超过3000次,其中包括菲尔兹奖获得者Drinfeld、Zelmanov和Borcherds以及著名数学家如Beilinson和Kac等人的重要引用。主持多项美国自然科学基金,并担任杂志Algebra Colloquium的主编以及Science China Mathematics等多个杂志的编委。
Meeting:128-767-072加入会议:
https://meeting.tencent.com/dm/hyMIOAPeEsWf
Deformations of Symplectic Foliations
Speaker: Marco Zambon (KU Leuven)
Time: 2022.03.04 20:00-22:00
Location: Zoom
ID:862 062 0549
Password:2022
Meeting:https://us02web.zoom.us/j/8620620549?pwd=bGhsaG15WjRza2V3ZEN4TzJYZ1FZQT09
Abstract:
Symplectic foliations and regular Poisson structures are the same thing. Taking the latter point of view, we exhibit an algebraic structure that governs the deformations of symplectic foliations, i.e. which allows to describe the space of symplectic foliations nearby a given one. Using this, we will address the question of when it is possible to prolong a first order deformation to a smooth path of symplectic foliations. We will be especially interested in the relation to the underlying foliation. This is joint work with Stephane Geudens and Alfonso Tortorella.
Bio:
Marco Zambon is an associate professor at KU Leuven, Belgium. He works on topics related to Poisson geometry, in particular on those related to foliations, deformations and Lie theory.
Diophantine approximations
Speaker:Nikolay Moshchevitin (Moscow State University)
Location:Zoom
ID:894 9789 1576
Password:237198
Lecture1. Continued fractions.
2022.01.19, 13:30-15:00
Representation of real numbers as continued fractions. Approximation by convergents, Perron's formula.
Irrationality measure function.
Lagrange and Dirichlet spectra. Minkowski diagonal continued fraction and the related spectrum. Geometry of continued fractions algorithm.
Lecture2. Distribution of Farey fractions.
2022.01.20, 13:30-15:00
Elements of basic number theory. Euler and Moebius functions.
Integral representation of greatest common divisor. Counting the number of reduced fractions in [0,1].
Fraenel's theorem. Relation to Riemann zeta-function.
Lecture3. Farey tree and Minkowski function.
2022.01.26, 13:30-15:00
Stern-Brocot sequences. Minkowski question-mark function.
Salem's theorem on the derivative. Fixed points problem. An analog to Fraenel's theorem.
Fourier-Stieltjes coefficients.
Lecture4.Multidimensional approximation.
2022.01.27, 13:30-15:00
Simultaneous approximation to real numbers. Linear forms close to xero.
Basic laws of approximation. Best approximations and phenomenon of degeneracy of dimension.
Diophantine exponents and Jarnik's inequalities.
Bio: Nikolay Moshchevitin教授现就职于莫斯科国立大学,研究兴趣为Geometry of numbers, geometric theory of Diophantine approximations, ergodic and combinatorial theory of numbers, theory of dynamical systems。共发表论文70余篇,超过400次引用。于1998年获得俄罗斯联邦国家奖。
Geometry of Gaussian random curves
Speaker:Andrey Dorogovtsev(Institute of Mathematics,NAS Ukraine)
Location:Zoom
ID:858 7772 7123
Password:803617
Abstract:
This course aims to provide a solid introduction on the geometry of Gaussian random curves. Since the theory of geometry of Gaussian random curves is based on the concept of Gaussian random process and fields, the first part of the course will be devoted to some properties of this process and fields. And the second part of the course is devoted to discussion of geometry of Gaussian random curves like the Self-intersection local times for planar Brownian motion and the hitting probabilities for planar Broownian motion. Professor Andrey will give students some time to understand the knowledge and give some small questions about the lecture.
Time:
Lecture 1: Gaussian random processes and fields. Main examples
In this lecture we give the definition of Gaussian random processes and fields. Also, we will give some examples to understand this.
Lecture 2: Smoothness of Gaussian random fields
In this lecture we discuss the smoothness of Gaussian random fields, and we can get some properties on Gaussian random fields.
Lecture 3: Euler characteristic of the subsets in Euclid space
In this lecture we give the definition of Euler characteristic which in defined on Euclid space, it is topological invariant.
Lecture 4: Rice formula and asymptotic of tales for supremum of Gaussian random fields
In this lecture we give the Rice formula and discuss the asymptotic of tales for supremum of Gaussian random fields.
Lecture 5: Trajectory of Brownian motion as a random curve. Basic properties
In this lecture we discuss the trajectory of Brownian motion and give some basic properties about this.
Lecture 6: Self-intersection local times for planar Brownian motion
In this lecture we discuss the investigation of the local times of self-intersection as the most important geometric characteristics for planar Brownian motion.
Lecture 7: Hitting probabilities for planar Brownian motion
In this lecture we discuss the hitting probabilities and how we use this to describe the trajectory of planar Brownian motion.
Lecture 8: Tube formula for planar Brownian motion
In this lecture we give the Tube formula for planar Brownian motion, and use it to help us learn the trajectory of Brownian motion.
Bio:
Andrey Dorogovtsev教授是乌克兰国家科学院通讯院士,乌克兰国家科学院数学所随机过程理论系主任,主要从事概率论及其相关领域研究,是乌克兰概率论研究方向学术领军人物之一。Andrey Dorogovtsev教授是乌克兰与德国、乌克兰与俄罗斯等国家联合项目的乌方负责人。同时,Andrey Dorogovtsev教授是《Theory of Stochastic Processes》、《Ukraine Mathematical Journal》等杂志的编委。
Knot theory
Speaker:Vassily Olegovich Manturov(Moscow Institute of Physics and Technology)
Time:2022年1月
Location:Tencent Meeting
Room Number:614-9548-1864
Password:372633
Abstract:
Lecture1.
Reidemeister moves. Colouring invariants, and the linking number.
2022/01/06 18:00-19:00
Abstract:
We will introduce diagrams of knots and links. We use the diagrams to build two invariants of links: Coloring invariant and the linking number.
Lecture2.
The Kauffman bracket, the Jones polynomial.
2022/01/09 18:00-19:00
Abstract:
We will use Kauffman bracket to prove that Jones polynomial is a link invariant.We will compute some examples and prove the Kauffman-Murasugi-Thistlethwaite Theorem.
Lecture3.
Fundamental group. The knot group.
2022/01/13 18:00-19:00
Abstract:
We will define a famous link invariant: the fundamental group of the knot complements. We will show that this group is not trivial if the knot is not trivial.
Lecture4.
The knot Quandle is a complete knot invariant.
2022/01/16 18:00-19:00
Abstract:
Matveev and Joyce defined a knot invariant, the knot quandle. This is a complete invariant. We can obtain many invariants from the knot quandle, for example, the knot group and coloring invariant.
Lecture5.
The braid groups
2022/01/20 18:00-19:00
Abstract:
We define the braid group. The action of the braid group on Aut(F_{n}) is complete.We will also discuss Markov Theorem and Alexander Theorem.
Lecture6.
The Alexander polynomial.
2022/01/23 18:00-19:00
Abstract:
We will introduce several ways to define the Alexander polynomial.
Lecture7.
Vassiliev invariant
2022/01/27 18:00-19:00
Abstract:
We will introduce the Vassiliev invariant and prove that “polynomial” invariant are all come from the Vassiliev invariant.
Lecture8.
Khovanov homology
2022/01/30 18:00-19:00
Abstract:
Khovanov homology is a categorification of the Jones polynomial, in the sense that its Euler characteristic is the Jones polynomial.
Bio:Professor Vassily Olegovich Manturov is from Moscow Institute of Physics and Technology. His research interest is low dimensional topology and knot theory. He has published more than 150 papers and got more than 1500 citations. He got "Professor of RAS" in 2016 and he is one of the Managing Editors of the "Journal of Knot Theory and Its Ramifications". He has published many books, for instance, 《Parity in knot theory and graph-links. Contemporary Mathematics. Fundamental Directions》,《Low-dimensional Topology and Combinatorial Group Theory》,《Virtual Knots. The State of the Art》 and 《Knot Theory》. He held many international conferences, such as "4-th Russian China Russia-China on Knot theory and Related topics" and three International Conferences in the Mathematical Institute (Oberwolfach) on knot theory and low-dimensional topology".
Rota-Baxter operators, skew braces and Yang-Baxter equation
Speaker:Valeriy Bardakov
Time:2021.12.17 15:00--17:00
Location:Zoom
Meeting ID: 862 062 0549
Password: 2021
Meeting:https://us02web.zoom.us/j/8620620549?pwd=NUhCMWpuTG9Od1RMNjhEdkdwTzlsUT09
Abstract:

Bio:Valeriy Bardakov is a professor of Sobolev Institute of Mathematics with holding a joint position at Laboratory of Topology and Dynamics of Novosibirsk State University. Valeriy Bardakov is a famous expert on braid theory, knot theory and group theory with over 90 publications in the area.
Variational Bihamiltonian Cohomology and Integrable Hierarchie
Speaker:Youjin Zhang(Tsinghua University)
Time:2021.12.10 10:00-12:00
Location:Meeting Tencent
Meeting ID:924-966-280
Meeting:https://meeting.tencent.com/dm/4PgMu2SMQi39
Abstract: In order to study deformations of Virasoro symmetries of the bihamiltonian integrable hierarchies associated to semisimple Frobenius manifolds, we introduce the notion of variational bihamiltonian cohomology, and compute the cohomology groups that will be used in our study of deformations of Virasoro symmetries. To illustrate its application, we classify the conformal bihamiltonian structures with semisimple hydrodynamic limits.
Bio:张友金,清华大学数学科学系教授,杰出青年基金获得者,教育部长江学者特聘教授。1994年于中国科技大学数学系获博士学位,1990-1991年在俄罗斯斯捷克洛夫数学所圣彼得堡分所作访问学者,1994-1999年在意大利国际理论物理中心、意大利国际高等研究院和日本京都大学数学系从事博士后研究,1999年起任清华大学数学科学系教授。主要从事数学物理与可积系统理论方面的研究,在双哈密顿可积方程簇的分类及其与Frobenius流形、Gromov-Witten不变量理论的联系等方面做出了重要的工作。在Invent. Math., CMP, Adv. Math.等顶尖杂志上发表学术论文50余篇。
O-operators on Lie infinity algebras
Speaker:Joana Nunes da Costa(University of Coimbra - Portugal)
Time:2021.12.03 16:00-18.00
Location:Zoom
ID:862 062 0549
Password:2021
ZOOM meeting:https://us02web.zoom.us/j/8620620549?pwd=NUhCMWpuTG9Od1RMNjhEdkdwTzlsUT09
Abstract: We define O-operators on a Lie infinity algebra E with respect to an action of E on another Lie infinity algebra. We characterize these operators as Maurer-Cartan elements of a certain Lie infinity algebra obtained by Voronov's higher derived brackets construction. We determine the Lie infinity algebra that controls the deformation of O-operators with respect to a fixed action.
Bio:Joana Nunes da Costa is a professor of University of Coimbra, Portugal. She mainly works on Poisson geometry and mathematical physics.
The Lang-Trotter Conjecture and the Hardy-Littlewood Conjecture
Speaker:Hourong Qin(Nanjing University)
Time:2021.11.26 09:00-11.00
Location:Meeting Tencent
Meeting ID:662 784 567
Meeting:https://meeting.tencent.com/dm/qloVYRjPFHvl

Bio: 秦厚荣教授现任南京大学数学系系主任,江苏国家应用数学中心主任,中国数学会常务理事,中国科学-数学编委,江苏省数学学会第十届,十一届理事长,第十二届监事会主席。1999年获得国家杰出青年基金,2004年受聘教育部长江学者计划特聘教授,首批入选国家“百千万人才计划”(2004年),享受国务院特殊津贴。他的研究方向主要是代数数论和代数K理论。他在同余数这一历史悠久问题上的研究上取得了重要成果;在数域的Tame核、Tate核方面做出了原创性工作,引发了大量后续工作;解决了田野,Browkin等人的多个猜想;在著名的椭圆曲线Anomalous素数的Mazur猜想以及Lang-Trotter猜想的研究中取得了突破。他在J. Reine Angew Math., P. London Math. Soc., Math. Ann. 等国际著名刊物上发表了数十篇论文,研究结果在国际同行中产生了广泛而积极的影响,被国外同行称为“秦的方法”,多次在高水平国际学术会议上作大会邀请报告。
Quantum GIM of N-fold affinization and quantum toroidal algebra
Speaker:Yun Gao(York University)
Time:2021.11.19 09:00-11.00
Location:Zoom
Meeting ID:862 062 0549
Password:2021
ZOOM meeting:https://us02web.zoom.us/j/8620620549?pwd=NUhCMWpuTG9Od1RMNjhEdkdwTzlsUT09
Abstract: Generalized intersection matrix (GIM) Lie algebras were introduced by Slodowy in the study of elliptic singularity. GIM Lie algebras of N-fold affinization were studied by Berman-Moody, Benkart-Zelmanov and among others. In this talk we will talk about quantum GIM algebras of N-fold affinization and quantum toroidal algebras.
Bio: 郜云教授是加拿大York大学教授,德国洪堡学者。主要研究方向是无穷维李(超)代数、量子群和表示理论。在高维仿射李代数研究领域做出了重要工作。他已在国际一流数学杂志上发表论文50余篇,其中包括两本美国数学会专著(Memoirs of American athematical Society 1997和2002)。
Embedding of Loday algebras into Rota-Baxter algebras
Speaker:Vsevolod Gubarev(Sobolev Institute of Mathematics,Novosibirsk State University)
Time:2021.11.12 15:00-17:00
Location:Zoom
Meeting ID:862 062 0549
Password:2021
ZOOM meeting:https://us02web.zoom.us/j/8620620549?pwd=NUhCMWpuTG9Od1RMNjhEdkdwTzlsUT09
Abstract:The classical Poincare–Birkhoff–Witt states that every Lie algebra injectively embeds into its universal enveloping associative algebra and this enveloping algebra in some sense does not depend on the Lie product (PBW-property). It is known that every Rota–Baxter algebra of weight 0/1 gives rise to a prealgebra/postalgebra. In 2013, it was proved that every pre- or postalgebra injectively embeds into appropriate Rota–Baxter algebra of weight 0 or 1 respectively. We study the structure and the PBW-property of the universal enveloping Rota–Baxter algebra of a pre- and post-Lie algebra.
Bio:Vsevolod Gubarev ,Senior researcher in Sobolev Institute of Mathematics and senior teacher in Novosibirsk State University (both in Novosibirsk, Russia). Area of interest: ring theory.
Rota-Baxter operators and non-skew-symmetric solutions of the classical Yang-Baxter equation on quadratic Lie algebras
Speaker:Maxim Goncharov (Sobolev Institute of Mathematics,Novosibirsk State University)
Time:2021.11.5 15:00-17:00
Location:Zoom
Meeting ID:862 062 0549
Password:2021
ZOOM meeting:https://us02web.zoom.us/j/8620620549?pwd=NUhCMWpuTG9Od1RMNjhEdkdwTzlsUT09
Abstract:Given a quadratic Lie algebra, it is well-known that skew-symmetric solutions of the classical Yang-Baxter equation are in one-to-one correspondence with skew-symmetric Rota-Baxter operators of weight zero. In this talk, we will study connections between Rota-Baxter operators of non-zero weight and non-skew-symmetric solutions of the classical Yang-Baxter equation on finite-dimensional quadratic Lie algebras. Particular attention will be given to the case of simple finite-dimensional Lie algebras.
Bio:Maxim Goncharov, Ph.D., Senior research fellow in Sobolev Institute of Mathematics, Associate Professor at Novosibirsk State University.
Revisiting and extending Poisson-Nijenhuis structures
Speaker:Henrique Bursztyn (Instituto Nacional de Matemática Pura e Aplicada)
Time:2021.10.22 08:00-09:00
Location:Zoom
Meeting ID:862 062 0549
Password:2021
ZOOM meeting:https://us02web.zoom.us/j/8620620549?pwd=NUhCMWpuTG9Od1RMNjhEdkdwTzlsUT09
Abstract:Poisson-Nijenhuis structures arise in various contexts, such as the theory of integrable systems and Poisson-Lie theory. I will revisit this notion from a new perspective and show how it can be extended to the realm of Dirac structures. I also hope to mention applications to integration problems. The talk is based on joint work with T. Drummond and C. Netto.
Bio:Henrique Bursztyn is a professor of Instituto Nacional de Matemática Pura e Aplicada (IMPA), Brazil. His research interest includes Poisson geomety, Dirac structures, Lie groupoids, Lie algebroids, deformation quantization and mathematical physics. He published more than 70 papers in high level journals, such as Duke Math. J, J. Reine Angew. Math., Compos. Math., Comm. Math. Phys., Int. Math. Res. Not. IMRN, Adv. Math.
Renormalization of quasisymmetric functions
Speaker:Li Guo (Rutgers University-Newark)
Time:2021.10.15 09:00
Location:Zoom
Meeting ID:862 062 0549
Password:2021
ZOOM meeting:https://us02web.zoom.us/j/8620620549?pwd=NUhCMWpuTG9Od1RMNjhEdkdwTzlsUT09
Abstract:The Hopf algebra of quasisymmetric functions (QSym) has played a central role in algebraic combinatorics and has broad applications. A natural linear basis of QSym is the set of monomial quasisymmetric functions defined by compositions, that is, vectors of positive integers. Extending such a definition for weak compositions, that is, vectors of nonnegative integers, leads to divergent expressions. This difficulty was addressed by a formal regularization in a previous work with Jean-Yves Thibon and Houyi Yu. Here we apply the method of renormalization in the spirit of Connes and Kreimer and realize weak composition quasisymmetric functions as power series. The resulting Hopf algebra has the Hopf algebra of quasisymmetric functions as both a Hopf subalgebra and a Hopf quotient algebra. It also gives a realization of free commutative Rota-Baxter algebra on one generator by weak quasisymmetric functions and thus addresses a question raise by Rota many years ago. This is a joint work with Houyi Yu and Bin Zhang.
Bio: 郭锂,美国罗格斯大学纽瓦克分校教授。郭锂博士于兰州大学获学士学位,于武汉大学获硕士学位,于华盛顿大学获博士学位,并在俄亥俄州立大学、普林斯顿高等研究院和佐治亚州大学作博士后。郭锂博士的数论工作为怀尔斯证明费马大定理的文章所引用,并将重整化这一物理方法应用于数学研究。他近年来推动Rota-Baxter代数及相关数学和数学物理的研究,应邀为美国数学会在“What Is”栏目中介绍Rota-Baxter代数,并出版这个领域的第一部专著。研究涉及结合代数,李代数,Hopf代数,operad,数论,组合,计算数学,量子场论和可积系统等广泛领域.
Title:Koszul duality: old and new
Speaker:Andrey Lazarev(University of Lancaster)
Time:2021.10.8 15:00
Location:Zoom
Meeting ID:862 062 0549
Password:2021
ZOOM meeting:https://us02web.zoom.us/j/8620620549?pwd=NUhCMWpuTG9Od1RMNjhEdkdwTzlsUT09
Abstract:Koszul duality is a phenomenon occurring in homological algebra and neighbouring fields, such as rational homotopy theory, representation theory, algebraic geometry, operads and operadic algebras. In this talk I will outline a modern approach to deformation theory based on Koszul duality and explain how it can be globalized.
Bio:Andrey Lazarev is a professor of pure mathematics in the University of Lancaster. His recent research deals with homotopy theory of differential graded algebras and categories, derived categories and higher phenomena. It has applications in rational homotopy theory, theory of operads and operadic algebras, algebraic topology and pure algebra. Andrey Lazarev is the Managing Editor of the journal《Bulletin of the London Mathematical Society》,as well as a Member of the Editorial Board of the journal《Higher_Structures》.
Previous lectures and talks: